ជំពូក ១: អនុគមន៍ប៉ោង (Convex Function)

October 2nd, 2020

From Wikipedia:

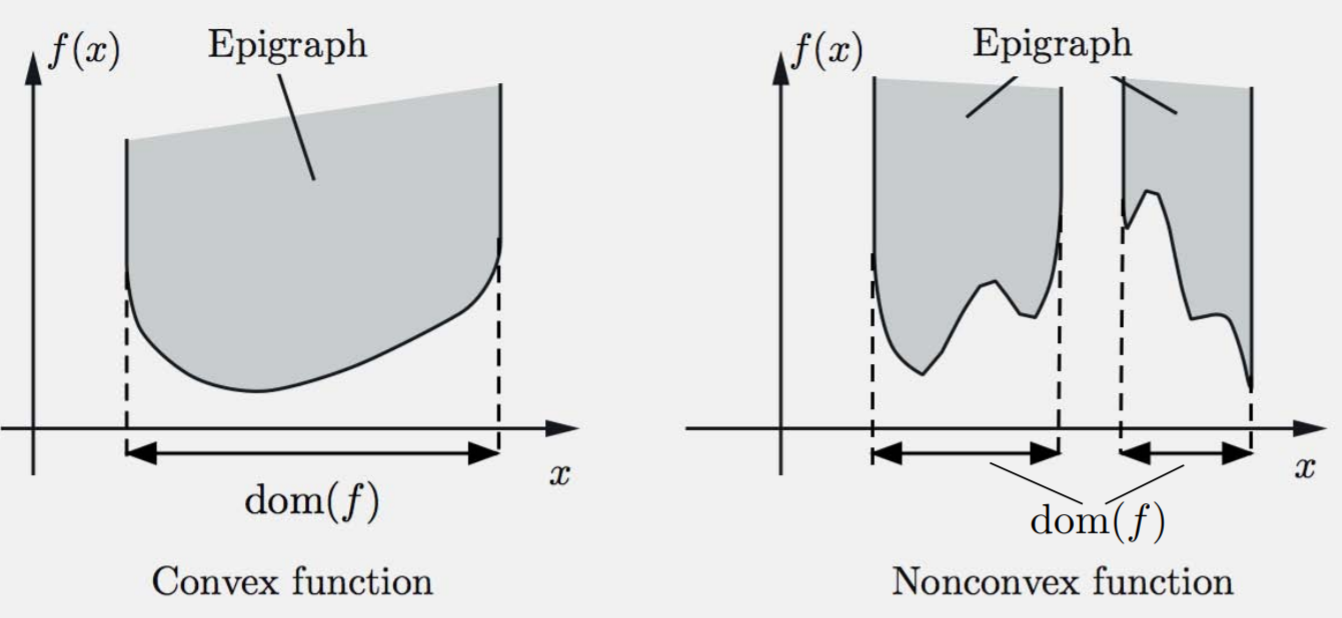
In mathematics, a real-valued function defined on an $n$-dimensional interval is called convex (or convex downward or concave upward) if the line segment between any two points on the graph of the function lies above or on the graph. Equivalently, a function is convex if its epigraph (the set of points on or above the graph of the function) is a convex set. A twice-differentiable function of a single variable is convex if and only if its second derivative is nonnegative on its entire domain. Well-known examples of convex functions of a single variable include the squaring function $x^2$ and the exponential function $e^{x}$.

គោលគំនិតគ្រឹះ

The Lagrange multiplier technique lets us find the maximum or minimum of a scalar field $f: \mathcal S \subseteq \mathbb{R}^n \longrightarrow \mathbb R$, when there is some constraints on the input values you are allowed to use.
This technique only applies to constraints that look something like this: $$g_i(x)=c_i, \quad \text{ where } x\in \mathbb{R}^n \text{ and } i = 1, \ldots, n$$ Here, $g_i$ is other scalar filed with the same input space as $f$ and $c_i$ is some constant.

Figure 1: The red curve shows the constraint $g(x, y) = c$. The blue curves are contours of $f(x, y)$. The point where the red constraint tangentially touches a blue contour is the maximum of $f(x, y)$ along the constraint, since $d_1 \geq d_2$.
The core idea is to look for points where the contour lines of $ f$ and $ g$ are tangent to each other.
This is the same as finding points where the gradient vectors of $f$ and $g$ are parallel to each other.
The entire process can be boiled down into setting the gradient of a certain function, called the Lagrangian , equal to the zero vector.

An $ n\times n$ symmetric real matrix which is neither positive semidefinite nor negative semidefinite is called indefinite.

Example - For what numbers $b$ is the following matrix positive semidefinite? \[ M = \left(\begin{array}{ccc} 2 & -1 & b \\ -1 & 2 & -1 \\ b & -1 & 2 \end{array}\right) \]

[Show proof]

ចម្លើយ. យក $x\in \mathbb{R}^3$ គេបាន៖ \begin{eqnarray*} x^T M x &=& (m\;\; n\;\; p)\begin{pmatrix} 2 & -1 & b \\ -1 & 2 & -1 \\ b & -1 & 2 \end{pmatrix} \begin{pmatrix} m\\ n\\ p \end{pmatrix} \\ &=& \begin{pmatrix} 2m-n+bp & -m+2n-p & bm-n+2p \end{pmatrix}\begin{pmatrix} m\\ n\\ p \end{pmatrix} \\ &=& m(2m-n+bp) + n(-m+2n-p) + p(bm-n+2p)\\ &=& 2m^2 - mn + bmp - mn + 2n^2 - np + bmp - np + 2p^2\\ &=& 2(m^2+n^2+p^2) + 2(bmp - mn - np) \end{eqnarray*}

1. Motivation

For general optimization problem (OP): \[ \begin{aligned} \min _{x \in \mathcal D}\; & f(x) \\ \text { s.t }\; & g_{i}(x) \leq 0, \quad i=1, \ldots, m\\ & h_{j}(x) =0, \quad j=1, \ldots, n \end{aligned} \qquad\qquad\tag{OP} \label{gen:op} \] ដែល $f, g_i$ និង $h_j$ គឺជាដែនស្កាលែរកំណត់ពី $\mathbb {R}^d \longrightarrow \mathbb R$ ។

វិធីសាស្ត្រ :

turn constrained problem into an unconstrained problem
the set of extremal points of the resulting unconstrained problem contains the extremal points of the original constrained problem (necessary condition). In some cases the two sets are equal (necessary and sufficient condition).
If we know

2. អនុគមន៍ឡាក្រង់ (Lagrange Function)

Definition 1: The Lagrangian or Lagrange function $ \operatorname{L}: \mathbb{R}^{d} \times \mathbb{R}_{+}^{m} \times \mathbb{R}^{n} \rightarrow \mathbb{R}$ associated with the $(\ref{gen:op})$ is defined as \[\operatorname{L}(x, \lambda, \mu) = f(x)+\sum_{j=0}^{r} \lambda_{j} g_{j}(x)+\sum_{i=0}^{s} \mu_{i} h_{i}(x) \] with $\mathcal{D}_{\operatorname{L}}= \mathcal{D} \times \mathbb{R}_{+}^{r} \times \mathbb{R}^{s}$ where $\mathcal D$ is the domain of the optimization problem. The variables $\lambda_{j}$ and $\mu_{i}$ are called Lagrange multipliers associated with the inequality and equality constraints.

By using the way of relaxation with indicator function, we can turn the constrained problem into an unconstrained problem : $$ I_{-}(x)= \begin{cases} 0&\mbox{if } x \leq \infty \\ \infty & \mbox{if } x > 0 \end{cases}, \quad \text { and } \quad I_{0}(x)=\left\{\begin{array}{cl} 0 & \text { if } x=0 \\ \infty & \text { if } x>0 \end{array}\right. $$ Thus, we get $$\min _{x \in \mathcal D} f(x) + \sum_{j=0}^{m} I_{-}\big(g_{j}(x)\big)+\sum_{i=0}^{n} I_{0}\big(h_{i}(x)\big)$$

2. Finite product topologies

Definition 2.1. Let $(X, \mathcal{T}_1)$ and $(Y, \mathcal{T}_2)$ be topological spaces. The product topology on $X \times Y$ is the topology generated by the basis \[ \mathcal{B}_{X\times Y} = \big\{U \times V: U \in \mathcal{T}_1, V \in \mathcal{T}_2\big\} \] More generally if $\left(X_{1}, \mathcal{T}_{1}\right), \ldots,\left(X_{n}, \mathcal{T}_{n}\right)$ are topological spaces, the product topology on \[ \prod_{i=1}^{n} X_{i} = X_{1} \times \cdots \times X_{n} \] is the topology generated by the basis \[ \mathcal{B}_{\prod_{i=1}^{n} X_{i}} = \big\{U_{1} \times U_{2} \times \cdots \times U_{n} \mid \; U_{i} \in \mathcal{T}_{i}, \; \text{ for all } i=1, \ldots, n\big\} \]

Simple as that. This definition is what you should want it to be, more or less. It is natural to expect that products of sets that are open in each coordinate should be open in the product. That alone does not give you a topology, it turns out, but it does give you a basis. So you generate a topology from it, and the result is the product topology. As you would expect, bases play nicely with this definition as well, as shown by the following easy proposition.

Proposition 2.2. Let $(X, \mathcal{T}_1)$ and $(Y, \mathcal{T}_2)$ be topological spaces, and let $\mathcal{B}_{X}$ and $\mathcal{B}_{Y}$ be bases on $X$ and $Y$ that generate $\mathcal{T}_1$ and $\mathcal{T}_2$, respectively. Then \[ \mathcal{B}=\left\{U \times V: U \in \mathcal{B}_{X}, V \in \mathcal{B}_{Y}\right\} \] is a basis for the product topology on $X \times Y$

Proof. $\mathcal{B}_{X} \subseteq \mathcal{T}$ and $\mathcal{B}_{Y} \subseteq \mathcal{U},$ and so every element of $\mathcal{B}$ is open in the product topology.
Now fix an open set $U$ in the product topology, and some point $(x, y) \in U .$ We need to find an element $B \in \mathcal{B}$ such that $x \in B \subseteq U .$ By definition of the product topology, there must be some $U_{X} \in \mathcal{T}$ and $U_{Y} \in \mathcal{U}$ such that $(x, y) \in U_{X} \times U_{Y} \subseteq U .$ Using the fact that $\mathcal{B}_{X}$ and $\mathcal{B}_{Y}$ are bases, find sets $B_{X} \in \mathcal{B}_{X}$ and $B_{Y} \in \mathcal{B}_{Y}$ such that $x \in B_{X} \subseteq U_{X}$ and $y \in B_{Y} \subseteq U_{Y} .$ But then we have: \[ (x, y) \in B_{X} \times B_{Y} \subseteq U_{X} \times U_{Y} \subseteq U \] so $B=B_{X} \times B_{Y}$ is the set we were looking for. Of course, this fact generalizes to larger finite products and the proof is similarly straightforward.

Barycentre de deux points

Définition 1: On appelle barycentre des points $A$ et $B$ ( ou $A$ et $B$ deux points du plan ou de I'espace ) affectés respectivement des coefficients $\alpha, \beta$ ( ou $\alpha, \beta$ sont des réels tels que $\alpha+\beta \neq 0$ l'unique point $G$ tel que $\alpha \overrightarrow{G A}+\beta \overrightarrow{G B}=\overrightarrow{0}$

ហាំ ការីម

Maths, Program, Music