ជំពូក៧ : លំហអាហ្វីន (Affine Spaces)
October 2nd, 2020
From Wikipedia:
ក្នុងលំហ $\mathbb {R}^{3}$ ប្លង់ $P_{2}$ ( ព័ណ៌ខៀវខាងលើ ) មិនមែនជាលំហវ៉ិចទ័ររងទេ តែវាជាលំហអាហ្វីនរង។ ទិសដៅរបស់វា គឺប្លង់ $P_{1}$ ( ព័ណ៌បៃតងនៅខាងក្រោម ) ដែលជាលំហវ៉ិចទ័ររង។ ទោះបី វ៉ិចទ័រ $\vec{a}$ និង $\vec{b}$ ស្ថិតក្នុង $P_{2}$ តែផលសងរបស់វា គឺជា វ៉ិចទ័រប្រាប់ទីតាំង : $\vec{a} - \vec{b} \notin P_{2}$ តែ $\vec{a} - \vec{b} \in P_{1}$ ។
ក្នុងគណិតវិទ្យា លំហអាហ្វីន (affine space) គឺជាទម្រង់ធរណីមាត្រមួយ ដែលកំណត់បានភាពទូទៅនៃលក្ខណៈរបស់ លំហអឺគ្លីដ (Euclidean spaces) តាមវិធីមួយដែលមិនអាស្រ័យទៅនឹងគោលគំនិតទាំងឡាយណាទាក់ទងនឹងចំងាយ និងរង្វាស់មុំ តែវារក្សាបានលក្ខណៈទាំងឡាយណា ដែលទាក់ទងនឹងភាពស្របគ្នា និងសមាមាត្រនៃប្រវែងរបស់អង្កត់ស្របគ្នា។
នៅក្នុងលំហអាហ្វីន គេមិនអាចធ្វើការបែងចែកភាពខុសគ្នានៃចំណុចគល់តម្រុយទាំងឡាយបានទេ។ ដូច្នេះ មិនមានវ៉ិចទ័រណាមួយ ដែលមានចំណុចគល់នៅនឹងថ្កល់នោះទេ ហើយក៏គ្មានវ៉ិចទ័រណាមួយ អាចភ្ជាប់បានតែមួយរបៀបគត់ទៅនឹងចំណុចមួយនោះដែរ។ ជំនួសមកវិញ ក្នុងលំហអាហ្វីន មានការបម្លាស់ទីតាំងនៃវ៉ិចទ័រ ដែលគេហៅថា វ៉ិចទ័របម្លែងកិល ឬត្រឹមតែ បម្លែងកិល រវាងពីរចំណុចក្នុងលំហ។ Thus it makes sense to subtract two points of the space, giving a translation vector, but it does not make sense to add two points of the space. Likewise, it makes sense to add a displacement vector to a point of an affine space, resulting in a new point translated from the starting point by that vector. We see that
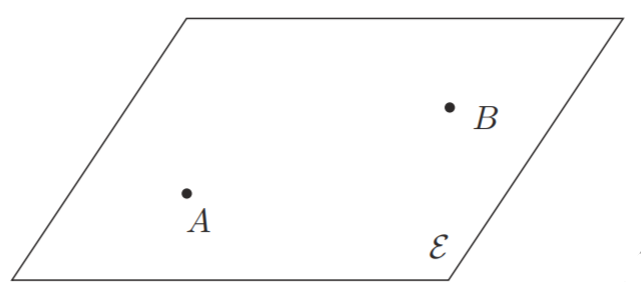
អំណេះតទៅ យើងសន្មតការកំណត់សរសេរអក្សរដិតត្រង់ $\E$ ឬ $\vect{\E}$ តាងអោយលំហវ៉ិចទ័រមួយកំណត់លើកាយ $\mathbb K$ (អាចជា $\R$ ឬ $\Cc$) ហើយបើសរសេរទ្រេត $A$ គឺតាងអោយចំណុចមួយរបស់លំហអាហ្វីន $\calE$ $-$ លើកលែងតែមានការកំណត់ផ្សេងពីនេះ នៅក្រោយទៀត។
- A
- B
និយមន័យ និង Notation
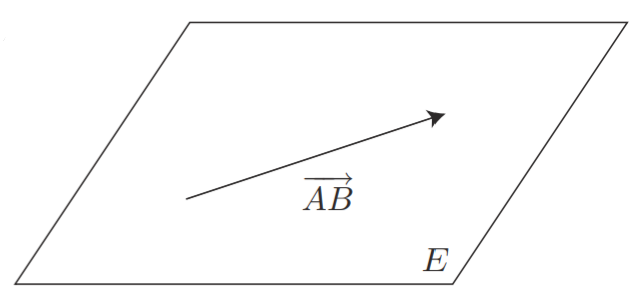
យក $\vect{\E}$ ជាលំហវ៉ិចទ័រកំណត់លើកាយ $\mathbb{R}$ និងកំណត់ $\mathcal{E}$ ជាសំណុំចំណុចមិនទទេ។ គេថា $\mathcal{E}$ ជា លំហអាហ្វីន ភ្ជាប់ទៅនឹងលំហវ៉ិចទ័រ $\vect{\E}$ (ឬតាមទិសដៅ $\vect{\E}$) បើមានអនុវត្តន៍មួយ $$ \begin{array}{rcl} \varphi:\; \mathcal{E}\times \mathcal{E} &\longrightarrow & \vect\E\\ (A,B) &\longmapsto & \overrightarrow{AB} \end{array} $$ ហៅថា difference function ដែលផ្ទៀងផ្ទាត់ស្វ័យសត្យ ដូចខាងក្រោម៖
- បើ $A\in \mathcal{E}$ ជាចំណុចនឹងមួយ នោះមានអនុវត្តន៍បង្រួមមួយ $\varphi_A = \varphi_{\big| {\{A\}\times \mathcal E}}$ ដែលកំណត់ដោយ៖ $$\begin{array}{rcl} \varphi_{\big|{\{A\}\times \mathcal E}}:\; \{A\}\times \mathcal{E} &\longrightarrow & \vect\E\\ (A,M) &\longmapsto & \vect{AM} \end{array}$$ ជាអនុវត្តន៍មួយទល់មួយ។
- ទំនាក់ទំនងហ្សាល (Relation de Chasles) $$\forall M, N, P\in \mathcal{E},\ \varphi(M,P) = \varphi(M,N) + \varphi(N,P)$$
លំហអាហ្វីន $\mathcal{E}$ ជា លំហមានវិមាត្ររាប់អស់ (finite dimensional space) បើលំហវ៉ិចទ័រ $\vect{\E}$ ជាលំហមានវិមាត្ររាប់អស់។ ក្នុងករណីនេះ វិមាត្ររបស់ $\mathcal{E}$ ស្មើនឹងវិមាត្ររបស់លំហទិសដៅ។
កំណត់សម្គាល់ :
- An affine space is basically a vector space without an origin.
- បើ $\mathcal{E}$ ជាលំហអាហ្វីន តាមទិសដៅ $\vect{\E}$ នោះធាតុរបស់ $\mathcal{E}$ ហៅថា ចំណុច ហើយគេកំណត់សរសេរដោយអក្សរធំ $A,B, C,\ldots $។
- ធាតុរបស់លំហ $\vect{\E}$ ហៅថា វ៉ិចទ័រ ហើយកំណត់សរសេរដោយអក្សរតូច មានសញ្ញាព្រួញនៅខាងលើ គឺ $\vec{i}, \vec{j}, \vec{k}, \vec{u}, \vec{v}, \cdots $។ ក្នុងករណីខ្លះទៀត គេសន្មតសរសេរវ៉ិចទ័រដោយមិនមានសញ្ញាព្រួញទេ!
- ជួនកាល គេតាងលំហអាហ្វីនដោយ $(\mathcal E, \vect{\E}, +)$ ហើយដើម្បីសម្រួលដល់ការយល់និយមន័យខាងលើ គេកំណត់បម្រែបម្រួលនិយមន័យផ្សេងមួយទៀត ដូចខាងក្រោម៖
គេហៅ $(\mathcal E, \vect{\E}, +)$ ជាលំហអាហ្វីន បើមានអនុវត្តន៍ : \[ \begin{array}{rcl} + :\; \mathcal E \times \vect{\E} &\longrightarrow & \mathcal E\\ (A, \vec v) &\longmapsto & A +\vec{v} \end{array} \] ដែលផ្ទៀងផ្ទាត់៖
- The zero vector acts as an identity: for all $A \in \mathcal E, A +\vec{0}= A$
- Addition of vectors correspond to translations: for all $A \in \mathcal E$ and $\vec{u}, \vec{v} \in \vect{\E}, A +(\vec{u}+\vec{v})=(A+\vec{u})+\vec{v}$
- For any $A, B \in \mathcal E$, there's a unique free vector $\vec{u} \in \vect{\E}$ such that $A+\vec{u}=B$
ចំណាំ: នៅក្នុងបរិបទខ្លះ ធាតុរបស់លំហវ៉ិចទ័រកំណត់លើកាយ $\mathbb{R}$ ត្រូវបានចាត់ទុកថាជា ចំណុច ឬជា វ៉ិចទ័រ ក៏បាន។
- បើ $\dim\big(\vect\E\big)=1$ នោះគេនិយាយថា $\mathcal{E}$ គឺជា បន្ទាត់អាហ្វីន។
- បើ $\dim\big(\vect\E\big)=2$ នោះគេថា $\mathcal{E}$ គឺជា ប្លង់អាហ្វីន។
- គ្រប់លំហវ៉ិចទ័រ $\vect{\E}$ កំណត់លើកាយ $\mathbb{R}$ តាមន័យកាណូនិច អាចចាត់ទុកថាជាលំហអាហ្វីនមួយ ដែលភ្ជាប់ទៅនឹងខ្លួនវា នៅពេលណាគេមានអនុវត្តន៍ដូចតទៅ៖ $$ \begin{array}{ccl} \vect\E\times \vect\E &\longrightarrow & \vect\E\\ (a,b) &\longmapsto & \vect{ab} = b-a \end{array} $$ ដែលផ្ទៀងផ្ទាត់ទៅនឹងលក្ខខណ្ឌនៃនិយមន័យខាងលើ។
ពិនិត្យសំណុំរង $\mathcal L$ របស់ $\mathbb R^2$ ដែលជាសំណុំចំណុចកំណត់ដោយ
$$\mathcal L=\bigl\{(x,y)\in \mathbb R^2\mid -x+y-2=0\bigr\}$$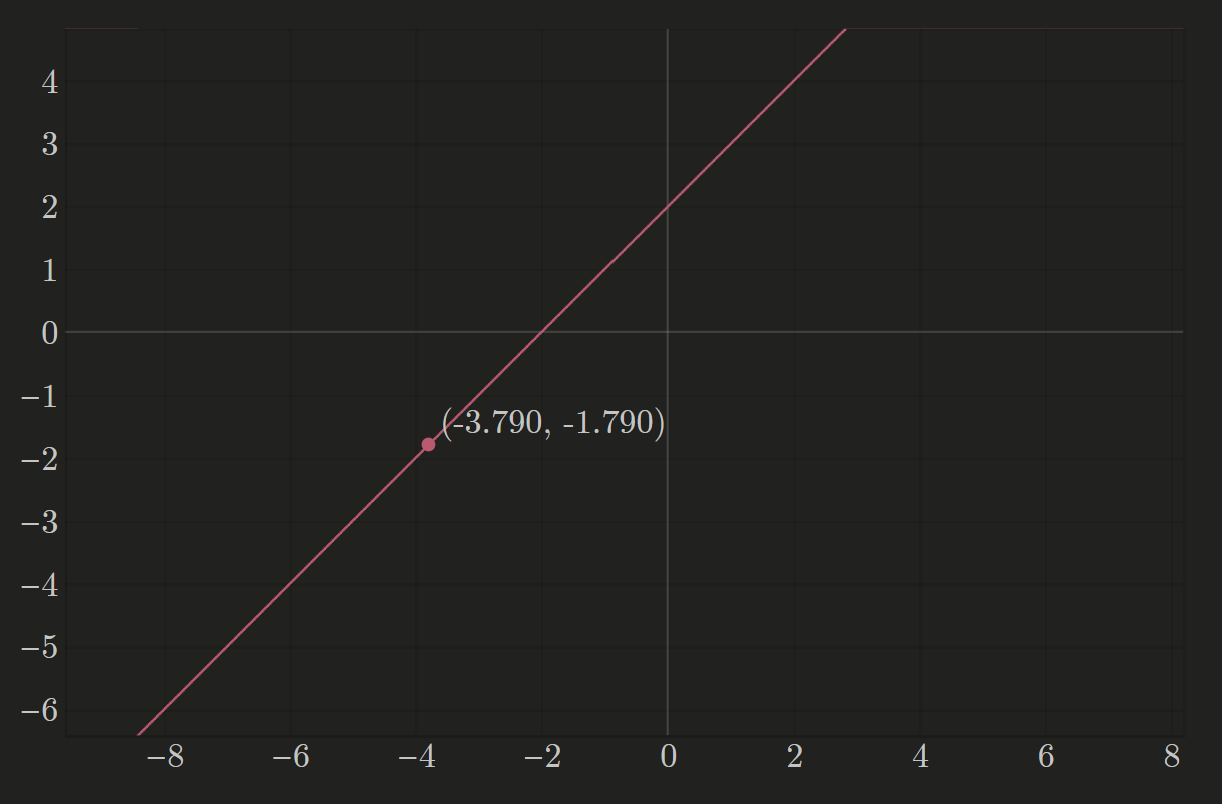
We can see that any point of the form $(x, y)=(x, 2+x)$, the line can be made into an affine space by defining $+: \mathcal L \times \mathbb R\rightarrow \mathcal L$, so that for any $u \in \mathbb R$ and any $P\in \mathcal L$:
\[
\begin{array}{rcl}
+ :\; \mathcal L\times \mathbb R &\longrightarrow & \mathcal L\\
\bigl(P, u\bigr) &\longmapsto & (x, 2+x)+u = (x+u, 2+x+u)
\end{array}
\]
For example the point $(-2,0)$ added with the vector $u=(1,1)$ results in the point $(-1,1)$ which belongs to the set $\mathcal L$.
Note that the vector space $\bbR$ is the line of equation $-x+y=0$, meaning that all vectors are parallel to $\vec u=(1,1)$.
វិធានគណនា
យក $\mathcal{E}$ ជាលំហអាហ្វីនភ្ជាប់ទៅនឹងលំហវ៉ិចទ័រ $\vect{\E}$ ។ ដូច្នេះគេបាន
- $\forall M, N \in \mathcal{E},\ \vect{AM}= \vect{AN}\Longrightarrow M = N$
- $\forall A, B \in \mathcal{E},\ \vect{AB} =\vect{0} \Longleftrightarrow A=B$
- $\forall A, B \in \mathcal{E},\ \vect{BA} = -\vect{AB}$
- $\forall A, B, C \in \mathcal{E},\ \vect{BC} = \vect{AC} - \vect{AB}$
- ចំពោះគ្រប់ចំណុច $A\in \mathcal{E}$ និងគ្រប់វ៉ិចទ័រ $\vect{u} \in \vect\E$ នោះមានចំណុចតែមួយគត់ $M\in \mathcal{E}$ ដែល $\vect{AM} = \vect{u}$
- បើ $A$ និង $B$ គឺជាចំណុចពីររបស់ $\mathcal{E}$ នោះមានវ៉ិចទ័រតែមួយគត់ $\vect{u}\in \vect\E$ ដែល $\vect{AB} = \vect{u}$
- តាមលក្ខណៈទី១ នៃនិយមន័យគេបានអនុវត្តន៍ \[\begin{array}{rrll} \phi: & \mathcal{E} &\longrightarrow &\vect\E\\ & M &\longmapsto &\phi(M) = \vect{AM} \end{array}\] គឺជាអនុវត្តន៍មួយទល់មួយ។ ដោយ $\varphi$ ជាអនុវត្តន៍ប្រកាន់ ដូច្នេះ គេទាញបានចម្លើយ។
- $(\Leftarrow)$ តាមទំនាក់ទំនងហ្សាល ចំពោះគ្រប់ $A\in \mathcal{E}$ គេបាន $$\vect{AA}+\vect{AA}=\vect{AA}\quad \text{ so } \quad \vect{AA}=\vect{0}$$ $(\Rightarrow)$ ដោយ $\vect{AB} = \vect{0} \Longrightarrow \vect{AB} = \vect{AA}$។ ដូច្នេះ $B=A$។
- ចំពោះគ្រប់ $A\in \mathcal{E}$ គេបាន $\vect{AA}= \vect 0$។ តាមទំនាក់ទំនងហ្សាល នោះ $\forall B\in \mathcal{E}$ គេបាន $\vect{AB} + \vect{BA} = \vect 0$។ ដូច្នេះ $\vect{BA} = -\vect{AB}$។
- $\forall A, B, C \in \mathcal{E}$ តាមទំនាក់ទំនងហ្សាល គេបាន $$ \vect{BC} = \vect{BA} + \vect{AC} = -\vect{AB} + \vect{AC} $$
- នៅពេលណាយើងកំណត់ចំណុច $A$ ឱ្យនៅថេរ នោះអនុវត្តន៍ \[ \begin{array}{rl} \phi: &\mathcal{E} \longrightarrow \vect\E\\ & M\longmapsto \vect{AM} \end{array} \] គឺជាអនុវត្តន៍មួយទល់មួយ។ ដូច្នេះ ចំពោះគ្រប់ $\vect u \in \vect\E$ នោះមានចំណុចតែមួយគត់ $M\in \mathcal{E}$ ដែល $\vect{AM} = \vect u$។
លក្ខណៈរបស់ប្រលេឡូក្រាម
សំណើ. ឧបមា $A, B, C$ និង $D$ គឺជាចំណុចបួននៅក្នុងលំហអាហ្វីន $\mathcal E$។ ដូច្នេះ លក្ខណៈខាងក្រោមសមមូលគ្នា៖
- $\vect{AB} = \vect{CD}$
- $\vect{AC} = \vect{BD}$
- $\vect{AB} + \vect{AC} = \vect{AD}$
បង្ហាញថា (i) $\Leftrightarrow$ (ii) \begin{eqnarray*} \vect{AB} =\vect{CD}\ &\Longleftrightarrow & \vect{AC} + \vect{CB} = \vect{CB} + \vect{BD}\\ &\Longleftrightarrow & \vect{AC} = \vect{BD} \end{eqnarray*} បង្ហាញថា (i) $\Leftrightarrow$ (iii) \begin{eqnarray*} \vect{AB} = \vect{CD} &\Longleftrightarrow & \vect{AB}=\vect{AD} - \vect{AC}\\ &\Longleftrightarrow & \vect{AB}+\vect{AC} = \vect{AD} \end{eqnarray*}
លំហអាហ្វីនរង
យក $\mathcal{E}$ ជាលំហអាហ្វីនភ្ជាប់នឹងលំហវ៉ិចទ័រ $\vect{\E}$។ គេថា សំណុំរងមិនទទេ $\mathcal{F}$ របស់ $\mathcal{E}$ គឺជាលំហអាហ្វីនរងរបស់ $\mathcal{E}$ បើមានចំណុចមួយ $A\in \mathcal{F}$ និងមានលំហវ៉ិចទ័ររងមួយ $\vect\F\subseteq \vect\E$ ដែល $$ \forall M \in \mathcal{E},\ M\in \mathcal{F} \Longleftrightarrow \vect{AM} \in \vect\F $$ ក្នុងករណីនេះ គេហៅ $\mathcal{F}$ គឺជាលំហអាហ្វីនរង ដែលកាត់តាមចំណុច $A$ និងតាមទិសដៅ $\vect\F$ ។
REMARK: It is said that a subset $\mathcal F$ of $\mathcal E$ is an affine subspace if $\mathcal F=\varnothing$ or $\mathcal F\ni A $ (a fixed point $A$) such that $\varphi_A\big(\mathcal F\big) = \vect\F$ is a vector subspace of $\vect\E$. It is easily proved that this vector subspace does not depend on the choice of the point $A$.
More precisely: If $\mathcal{F}$ is an affine subspace through $A$ directed by $\vect\F$, then
$$\varphi_{A}(\mathcal{F})=\vect\F \qquad\text{ and }\qquad
\mathcal{F}=\bigl\{M \in \mathcal{E} \mid\, \overrightarrow{A M} \in \vect\F\bigr\}
$$
ចំពោះគ្រប់ចំណុច $A\in \mathcal{E}$ សំណុំដែលមានតែមួយធាតុ $\{A\}$ គឺជាលំហអាហ្វីនរងរបស់ $\mathcal{E}$។ វាគឺជាលំហអាហ្វីនរងរបស់ $\mathcal{E}$ ដែលកាត់តាមចំណុច $A$ និងតាមទិសដៅ $\vect\F=\{\vect 0\}$។
យក $\vect{\E}$ ជាលំហវ៉ិចទ័រមួយកំណត់លើកាយ $\mathbb{R}$។ ដូច្នេះ ចំពោះគ្រប់លំហអាហ្វីនរង $\mathcal{F}$ របស់ $\vect{\E}$ មានចំណុចមួយ $\vec a\in \vect\E$ និងមានលំហវ៉ិចទ័ររងមួយ $\vect\F \subseteq \vect\E$ ដែល
$$
\mathcal{F} = \vec a + \vect\F
$$
ដូច្នេះ គ្រប់លំហវ៉ិចទ័ររងរបស់ $\vect{\E}$ អាចចាត់ទុកដូចជាលំហអាហ្វីនរងរបស់ $\vect{\E}$ ដែរ។ តែករណីច្រាសមកវិញ មិនពិតជាទូទៅនោះទេ។
ជាការពិត បើយក $\mathcal{F}$ ជាលំហអាហ្វីនរងរបស់ $\vect{\E}$ នោះតាមនិយមន័យ គេមានចំណុចមួយ $a\in \mathcal{F}$ និងលំហវ៉ិចទ័ររងមួយរបស់ $\vect{\E}$ (គឺ $\vect\F \subseteq \vect\E$) ដែល \begin{eqnarray*} \forall\; x\in \vect\E,\ x\in \mathcal{F}&\Longleftrightarrow & x - a\in \vect\F\\ &\Longleftrightarrow & x\in (a + \vect\F) \end{eqnarray*} ដូច្នេះ $\mathcal{F} = a + \vect\F$
យក $\mathcal{F}$ គឺជាលំហអាហ្វីនរងរបស់ $\mathcal{E}$ ដែលកាត់តាមចំណុច $A$ និងតាមទិសដៅ $\vect\F$។
- បើ $\dim\big(\vect\F\big)=1$ ដែល $\vect\F = \text{\bf Vect}(\vec{u})$ គេបាន $\mathcal{F}$ គឺជា បន្ទាត់អាហ្វីន របស់លំហ $\mathcal{E}$ ដែលកាត់តាមចំណុច $A$ និងតាមទិសដៅវ៉ិចទ័រ $\vec{u}$ ។ គេតាងវាដោយ $\calD\big(A,\vec{u}\big)$។ ដូច្នេះ ចំពោះគ្រប់ $M\in \mathcal{F}$ គេបាន \begin{eqnarray*} M\in \calD\bigl(A,\vec{u}\bigr) &\Longleftrightarrow & \Big\{\vect{AM},\vec{u}\Big\} {\text{ l.d }}\\ &\Longleftrightarrow & \exists \alpha\in \mathbb{R}:\ \vect{AM}=\alpha\vec{u} \end{eqnarray*}
- បើ $\dim\big(\vect\F\big)=2$ ដែល $\vect\F = \text{\bf Vect}\left(\vec{u}, \vec{v}\right)$ នោះគេថា $\mathcal{F}$ គឺជា ប្លង់អាហ្វីន ដែលកាត់តាមចំណុច $A$ និងតាមវ៉ិចទ័រប្រាប់ទិសដៅ $\vec{u}$ និង $\vec{v}$ ។ គេតាងវាដោយ $\calP\left(A,\vec{u},\vec{v}\right)$។ ដូច្នេះ ចំពោះ $M\in \mathcal{F} $ គេបាន \begin{eqnarray*} M\in \calP\left(A,\vec{u}, \vec{v}\right) &\Longleftrightarrow & \bigl\{\vect{AM},\vec{u},\vec{v}\bigr\} {\text{ l.d }}\\ &\Longleftrightarrow & \exists(\alpha,\beta) \in \mathbb{R}^{2}:\ \vect{AM}= \alpha\vec{u} + \beta\vec{v} \end{eqnarray*}
-
បើលំហវ៉ិចទ័ររង $\vect\F$ គឺជាអ៊ីពែរប្លង់ (hyperplan) របស់ $\vect{\E}$ នោះគេថា $\mathcal{F}$ គឺជា អ៊ីពែរប្លង់អាហ្វីន មួយរបស់ $\mathcal{E}$ ។
ដោយ $\vect\F$ គឺជាអ៊ីពែរប្លង់មួយរបស់ $\vect{\E}$ នោះគេរកបានទម្រង់លីនេអ៊ែរមួយ មិនទទេ $\varphi$ កំណត់លើ $\vect\E$ ដែលគ្រប់ $\vec u \in \vect\E$ គេបាន ៖ \[ \vec u \in \vect\F \Longleftrightarrow \varphi\bigl(\vec u\bigr) = 0 \] ដូច្នេះ អ៊ីពែរប្លង់អាហ្វីន $\calF$ នឹងកំណត់ដោយ គ្រប់ $M\in\calE$ គេបាន ៖ \[\fcolorbox{red}{yellow}{\quad \color{Green}$ M \in \calF \Longleftrightarrow \varphi\Big(\vect{AM}\Big) = 0$ \quad} \]
NOTE: យក $\mathcal{F}$ គឺជាលំហអាហ្វីនរងរបស់ $\mathcal{E}$ ដែលកាត់តាមចំណុច $A$ និងតាមទិសដៅ $\vect\F$។ ដូច្នេះ ចំពោះគ្រប់ចំណុច $B\in \mathcal{F}$ គេបាន $$ \forall\; M\in \mathcal{E},\ M\in \mathcal{F}\Longleftrightarrow \vect{BM}\in \vect\F $$
យក $\mathcal{E}$ ជាលំហអាហ្វីន តាមទិសដៅនៃលំហវ៉ិចទ័រ $\vec{E}$។
- គេថា ចំណុចទាំងឡាយរបស់លំហអាហ្វីន $\mathcal{E}$ កូលីនេអ៊ែរគ្នា (រត់ត្រង់គ្នា) បើចំណុចទាំងនោះស្ថិតនៅលើបន្ទាត់អាហ្វីនតែមួយ។
- គេថា ចំណុចទាំងឡាយរបស់លំហអាហ្វីន $\mathcal{E}$ កូប្លានែរគ្នា (នៅលើប្លង់តែមួយ) បើចំណុចទាំងនោះស្ថិតនៅលើប្លង់អាហ្វីនតែមួយ។
ប្រសព្វនៃពីរលំហអាហ្វីនរង
យក $\mathcal{E}$ ជាលំហអាហ្វីន តាមទិសដៅ $\vect{\E}$។ កំណត់ $\mathcal{F}$ និង $\mathcal{G}$ ជាលំហអាហ្វីនរងពីររបស់ $\mathcal{E}$ តាមទិសដៅផ្សេងគ្នា $\vect\F$ និង $\vect\G$។ ដូច្នេះ ប្រសព្វរវាងលំហ $\mathcal{F}$ និង $\mathcal{G}$ (បើសិនជាមិនទទេ) គឺជាលំហអាហ្វីនរងរបស់ $\mathcal{E}$ តាមទិសដៅ $\vect\F\cap \vect\G$។
Proof: ឧបមាថា $\mathcal{F}\cap \mathcal{G}\neq\varnothing$ និងយក $A\in \mathcal{F}\cap \mathcal{G}$។ គេបាន \begin{eqnarray*} M\in \mathcal{F}\cap \mathcal{G} &\Longleftrightarrow & M \in \mathcal{F}\ \text{ and }\ M\in\mathcal{G}\\ &\Longleftrightarrow & \vect{AM}\in \vect\F \ \text{ and }\ \vect{AM}\in \vect\G\\ &\Longleftrightarrow & \vect{AM} \in {\vect\F} \cap {\vect\G} \end{eqnarray*} ដូច្នេះ $\mathcal{F}\cap \mathcal{G}$ គឺជាលំហអាហ្វីនរង តាមទិសដៅ $\vect\F\cap \vect\G$។
-
បើ $\mathcal{D}$ និង $\mathcal{D}'$ ជាបន្ទាត់អាហ្វីនពីររបស់ $\mathcal{E}$ នោះគេបានលក្ខខណ្ឌមួយក្នុងចំណោមលក្ខខណ្ឌខាងក្រោមផ្ទៀងផ្ទាត់៖
- $\mathcal{D}\cap \mathcal{D}'=\varnothing$
- $\mathcal{D}\cap \mathcal{D}'$ បង្រួមមកនៅមួយចំណុចរបស់ $\mathcal{E}$
- $\mathcal{D}=\mathcal{D}'$
-
បើ $\mathcal{P}$ និង $\mathcal{P}'$ ជាប្លង់អាហ្វីនពីររបស់ $\mathcal{E}$ នោះគេបានលក្ខខណ្ឌមួយក្នុងចំណោមលក្ខខណ្ឌខាងក្រោមផ្ទៀងផ្ទាត់៖
- $\mathcal{P}\cap \mathcal{P}'=\varnothing$
- $\mathcal{P}\cap \mathcal{P}'$ បង្រួមមកនៅបន្ទាត់អាហ្វីនមួយ
- $\mathcal{P}=\mathcal{P}'$
-
បើ $\mathcal{D}$ ជាបន្ទាត់អាហ្វីនមួយលើ $\mathcal{E}$ និង $\mathcal{P}$ ជាប្លង់អាហ្វីនមួយលើ $\mathcal{E}$ នោះគេបានលក្ខខណ្ឌមួយក្នុងចំណោមលក្ខខណ្ឌខាងក្រោមផ្ទៀងផ្ទាត់៖
- $\mathcal{D}\cap \mathcal{P} = \varnothing$
- $\mathcal{D}\cap \mathcal{P}$ បង្រួមមកនៅចំណុចមួយរបស់ $\mathcal{E}$
- $\mathcal{D} \subseteq \mathcal{P}$
យក $\calE$ ជាលំហអាហ្វីនតាមទិសដៅ $\vect\E$ ហើយ $\calF$ និង $\calG$ ជាលំហអាហ្វីនរងពីររបស់ $\calE$ តាមទិសដៅ $\vect\F$ និង $\vect\G$ រៀងគ្នា ដែល $\calF \cap \calG \neq \varnothing$។
- បើ $\vect\F \subseteq \vect\G$ នោះគេបាន $\calF \subseteq \calG$
- បើ $\vect\F = \vect\G$ នោះគេបាន $\calF = \calG$
Proof:
-
ឧបមាថាថា $\vect\F \subseteq \vect\G$ នោះយើងនឹងបង្ហាញថា $\calF\subseteq \calG$?
យក $A \in \calF \cap \calG$ និងកំណត់ $M \in \calF$ ។ គេបាន $\vect{AM}\in \vect\F$ ហើយដោយ $\vect\F \subseteq \vect\G$ នោះគេបាន $\vect{AM}\in\vect\G$ ។ ដូច្នេះ $M \in\calG$ ។ -
បើ $\vect\F = \vect\G$ នោះគេបាន $\vect\F\subseteq \vect\G$ និង $\vect\G\subseteq \vect\F$ ។
តាមលក្ខណៈ (១.) ខាងលើ គេបាន $\calF \subseteq \calG$ និង $\calG\subseteq \calF$ ។ ដូច្នេះ $\calF = \calG$ ។
គេបានលក្ខខណ្ឌដូចខាងក្រោម៖
- យក $\mathcal{E}$ ជាលំហអាហ្វីនទូទៅ និងកំណត់ $\mathcal{F}$ និង $\mathcal{G}$ ជាលំហអាហ្វីនរងពីររបស់ $\mathcal{E}$ តាមទិសដៅផ្សេងគ្នា $\vect \F$ និង $\vect \G$។ គេបាន $$\fbox{$ \mathcal{F}\cap\mathcal{G} \neq \varnothing\quad \Longleftrightarrow \quad \exists(A,B) \in \mathcal{F}\times \mathcal{G}:\ \vect{AB}\in \vect{\F} + \vect{\G}$ } $$
- ឧបមា $\mathcal{E}$ ជាលំហអាហ្វីនមានវិមាត្រ $3$ និងកំណត់ $\mathcal{D}$ ជាបន្ទាត់អាហ្វីនមួយលើ $\mathcal{E}$ តាមវ៉ិចទ័រទិសដៅ $\vect{u}$ ហើយ $\mathcal{P}$ ជាប្លង់អាហ្វីនមួយលើ $\mathcal{E}$ តាមទិសដៅវ៉ិចទ័រ $\vect{v}$ និង $\vect{w}$។ ដូច្នេះ គេបាន $\mathcal{D}\cap\mathcal{P}$ បង្រួមមកនៅត្រឹមមួយចំណុច លុះត្រាតែប្រព័ន្ធវ៉ិចទ័រ $\left\{\vect{u},\vect v,\vect w\right\}$ មិនអាស្រ័យលីនេអ៊ែរគ្នា។
Proof: ពិនិត្យមើលលក្ខខណ្ឌចាំបាច់ និងគ្រប់គ្រាន់ ដូចខាងក្រោម៖
-
$(\Longrightarrow)$ ឧបមាថា $\mathcal{F}\cap \mathcal{G}\neq\varnothing$ និងយក $\Omega\in\mathcal{F}\cap \mathcal{G}$ គេបាន៖
$$\forall A\in \mathcal{F}, \forall B\in \mathcal{G}:\ \vect{A\Omega} \in \vect \F \ {\text{ និង } } \ \vect{B\Omega}\in \vect \G$$
ដូច្នេះ $\vect{A\Omega} - \vect{B\Omega}\in \vect\F+\vect \G$ ដោយ $\vect{A\Omega}-\vect{B\Omega}=\vect{AB}$។ ដូច្នេះ $\vect{AB}\in \vect\F+\vect\G$។
$(\Longleftarrow)$ ឧបមាថា គេមាន $(A,B)\in \mathcal{F}\times\mathcal{G}$ ដែល $\vect{AB}\in \vect \F+\vect \G$។ ដូច្នេះ គេមាន $\left(\vect{u}, \vect{v}\right)\in \vect\F\times \vect\G$ ដែល $\vect{AB}=\vect{u} + \vect{v}$។
យកចំណុច $M\in\mathcal{F}$ ដែល $\vect{AM}=\vect{u}$ និង $N\in\mathcal{G}$ ដែល $\vect{BN}=-\vect{v}$។ គេបាន \begin{eqnarray*} \vect{AM} = \vect{u}&\Longrightarrow & \vect{AB}+\vect{BM} = \vect{u}\\ &\Longrightarrow & \vect{BM} = -\vect{v}\\ &\Longrightarrow & \vect{BM} = \vect{BN}\\ &\Longrightarrow & M=N \end{eqnarray*} ដូច្នេះ $M\in \mathcal{F}\cap \mathcal{G}$។ គេទាញបាន $\mathcal{F}\cap \mathcal{G}\neq\varnothing$។ -
$(\Longrightarrow)$ ឧបមាថា $\mathcal{D}\cap \mathcal{P}$ បង្រួមមកនៅត្រឹមចំណុចមួយ $A\in\mathcal{E}$ និងសន្មត់តាមវិធីផ្ទុយពីការពិតថា $\left\{\vect{u},\vect{v},\vect{w}\right\}$ ជាប្រព័ន្ធអាស្រ័យលីនេអ៊ែរគ្នា។ ដោយ $A\in \mathcal{D}$ នោះគេមានចំណុចមួយ $B\in \mathcal{D}$ ដែល $\vect{AB}=\vect{u}$។ ដូច្នេះ $\left\{\vect{AB}, \vect{v},\vect{w}\right\}$ អាស្រ័យលីនេអ៊ែរគ្នា។ ហើយ $A\in \mathcal{P}$ នោះគេបាន $B\in \mathcal{P}$។ គេបាន $B\in \mathcal{D}\cap \mathcal{P}$។ ដែលនេះផ្ទុយពីការពិត ព្រោះ $A\neq B$។
$(\Longleftarrow)$ ឧបមាថា $\left\{\vect{u},\vect{v}, \vect{w}\right\}$ មិនអាស្រ័យលីនេអ៊ែរគ្នា។ ដោយ $\dim(E)=3$ ដែល $\vect{\E}$ ជាទិសដៅរបស់លំហ $\mathcal{E}$ នោះគេបាន $E = \Vect{\vect{u}} + \Vect{\{\vect{v},\vect{w}\}}$។ ដូច្នេះ $\vect{AB}\in \Vect{\vect{u}} + \Vect{\{\vect{v},\vect{w}\}}$ នោះតាមលក្ខខណ្ឌ i) គេបាន៖ $\mathcal{D}\cap \mathcal{P} \neq \varnothing$។
ឧបមាថា $\mathcal{D}\cap \mathcal{P}$ ផ្ទុកធាតុច្រើនជាងមួយចំណុច និងយក $A$ និង $B$ ជាចំណុចពីរផ្សេងគ្នារបស់ $\mathcal{D}\cap \mathcal{P}$ គេបាន ៖ \[ \begin{cases} \vect{AB} = a\vect{u} & \ \text{ since }\ a\neq 0\\ \vect{AB} = b\vect{v} + c \vect{w}& \end{cases} \] ដូច្នេះ $a\vect{u} - b\vect{v} - c\vect{w}= \vect{0}$ ដែល $a\neq 0$។ គេបាន $\left\{\vect{u},\vect{v},\vect{w}\right\}$ អាស្រ័យលីនេអ៊ែរគ្នា ដែលផ្ទុយពីការពិត។ ដូច្នេះ $\mathcal{D}\cap \mathcal{P}$ បង្រួមមកនៅត្រឹមតែមួយចំណុច។
ភាពស្របគ្នានៃពីរលំហអាហ្វីនរង
ឧបមា $\mathcal{E}$ ជាលំហអាហ្វីនមួយតាមទិសដៅ $\vect{\E}$ និងកំណត់ $\mathcal{F}$ និង $\mathcal{G}$ ជាលំហអាហ្វីនរងពីរតាមទិសដៅរៀងគ្នា $\vect\F$ និង $\vect\G$។ គេថា \[ \mathcal{F} \text{ is parallel to } \mathcal G \quad \text{ if } \quad \vect\F\subseteq \vect\G \quad \text{or }\quad \vect\G\subseteq \vect\F \]
- ក្នុងករណីដែល $\vect\F=\vect\G$ គេថា $\mathcal{F}$ និង $\mathcal{G}$ ជាលំហស្របគ្នាដាច់ខាត។
- បើ $\mathcal{F}$ និង $\mathcal{G}$ ស្របគ្នា នោះគេតាងដោយ $\mathcal{F}\ \Vert\ \mathcal{G}$។
- យក $\mathcal{D} = D\left(A,\vect{u}\right)$ និង $\mathcal{D}' = D\left(B, \vect{v}\right)$ ជាបន្ទាត់អាហ្វីនពីររបស់ $\mathcal{E}$។ ដូច្នេះ $$\fcolorbox{Red}{blue!5}{$\mathcal{D}\ \Vert\ \mathcal{D}' \Longleftrightarrow \left\{\vect{u}, \vect{v}\right\}\ \ \text{ l.d } $} $$
- $\mathcal{P} = P\left(A, \vect v,\vect w\right)$ និង $\mathcal{P}' = P\left(B,\vect v',\vect w'\right)$ ជាប្លង់អាហ្វីនពីររបស់ $\mathcal{E}$។ គេបាន $$\fcolorbox{Red}{blue!5}{$\mathcal{P}\ \Vert\ \mathcal{P}' \Longleftrightarrow \left\{\vect{v}, \vect{v}', \vect w'\right\} { \text{ and } }\left\{\vect{w}, \vect{v}', \vect w'\right\}\ \ \text{ l.d }$} $$
លំហអាហ្វីនរងបង្កដោយសំណុំចំណុច
យក $\mathcal{E}$ ជាលំហអាហ្វីនភ្ជាប់ទៅនឹងលំហវ៉ិចទ័រ $\vect{\E}$ និង $\mathcal{A}$ គឺជាផ្នែកមួយមិនទទេរបស់ $\mathcal{E}$ និងកំណត់ $A\in\mathcal{A}$។ គេហៅ លំហអាហ្វីនរងបង្កដោយ $\mathcal{A}$ ដែលតាងដោយ $\mathbf{Aff}\big(\calA\big)$ គឺជាលំហអាហ្វីនរងរបស់ $\mathcal{E}$ ដែលកាត់តាមចំណុច $A$ និងតាមទិសដៅ $$\fbox{\color{blue}$\quad \vect\F = \Vect{\vect{AB}\;\mid \ B\in\mathcal{A}}\quad$}$$
NOTE:
$\Aff{\calA}$ គឺជាលំហអាហ្វីនរងតូចបំផុតរបស់ $\mathcal{E}$ ដែលផ្ទុក $\mathcal{A}$។ មានន័យថា បើ $\mathcal{F}$ គឺជាលំហអាហ្វីនរងរបស់ $\mathcal{E}$ ដែលផ្ទុក $\mathcal{A}$ នោះ $\mathcal{F}$ ផ្ទុក $\Aff{\calA}$។
ជាការពិត គេកំណត់យកចំណុចមួយ $A\in\mathcal{A}$ និងតាង $\vect\F$ គឺជាទិសដៅរបស់ $\mathcal{F}$។ ដូច្នេះ ដោយ $M\in \Aff{\calA}$ នោះតាមនិយមន័យ គេមាន $(A_{1},A_{2}, \ldots,A_{m})\in \mathcal{A}^{m}$ និងមាន $(\alpha_{1}, \alpha_{2},\ldots, \alpha_{m})\in \mathbb{R}^{m}$ ដែល
$$
\vect{AM} = \sum_{i=1}^{m}\alpha_{i}\vect{AA_{i}}
$$
ឬម្យ៉ាងទៀត ចំពោះគ្រប់ $i\in\{1, 2, \cdots, m\}$ គេបាន $A_{i}\in \mathcal{F}$ និង $A\in \mathcal{F}$។ ដូច្នេះ គ្រប់ $i\in\{1, 2, \cdots, m\}$ គេបាន $\vect{AA_{i}} \in \vect\F$។ ដូច្នេះ $\vect{AM}\in \vect\F$។ គេទាញបាន $M\in \mathcal{F}$។
បីចំណុច $A, B$ និង $C$ របស់លំហអាហ្វីន $\mathcal{E}$ ជាចំណុចរត់មិនត្រង់គ្នា បើប្រព័ន្ធ $\left\{\vect{AB},\vect{AC}\right\}$ មិនអាស្រ័យលីនេអ៊ែរ។
- Let $T: \mathbf U\longrightarrow \mathbf V$ is a linear map where $\mathbf U$ and $\mathbf V$ are $\mathbb K$-v.s. Show that $T^{-1}(v)$ for any $v\in \mathbf V$ is an affine subspace of the affine space $\mathbf U$ having that $\mathrm{ker}(T)$ is its direction. Moreover, show that $T^{-1}(v)$ is parallel to every other $T^{-1}(v')$ for $v, v' \in \mathbf V$.
- Let $\mathbf E$ be vector space of polynomial function with degree at most $2$ where its value is $0$ at $1$ $$ \mathbf E=\bigg\{\, f: \mathbb{R} \rightarrow \mathbb{R} \mid f(x) = a x^{2}+b x+c \text { for } x \in \mathbb{R}\;\bigg\} $$ and $a+b+c=0$. Then, let $\mathcal{A}$ be the set of polynomial function with degree at most $2$ as follows $$ \mathcal{A}=\bigg\{\;F: \mathbb{R} \rightarrow \mathbb{R} \mid F(x) = a x^{2}+b x+c \text { for } x \in \mathbb{R}\;\bigg\} $$ and $ a+b+c=3$. Show that $\mathcal A$ is an affine space with $\mathbf E$ is its direction space.
-
Let consider in $\mathbb{R}^{3}$ with given points
$$
A=\left(\begin{array}{l}
0 \\
2 \\
1
\end{array}\right), B=\left(\begin{array}{l}
1 \\
0 \\
1
\end{array}\right), C=\left(\begin{array}{c}
1 \\
-1 \\
0
\end{array}\right), D=\left(\begin{array}{l}
1 \\
2 \\
3
\end{array}\right), E=\left(\begin{array}{l}
3 \\
3 \\
2
\end{array}\right)
$$
- Show that the points $A, B$ and $C$ are not aligned, we denote by $\mathcal{P}$ the generated affine plane by these three points. Give an equation of $\mathcal{P}$. 😇
- We denote by $\mathcal{D}$ the line generated by the points $D$ and $E$. Give a system of equations of the line $\mathcal{D}$.
- Find the point $M$ where $\{M\} = \mathcal{D} \cap \mathcal{P}$. 😂
បារីសង់ - Barycentre
អនុគមន៍វ៉ិចទ័រ Leibnitz
ឧបមាថា $\mathcal{E}$ គឺជាលំហអាហ្វីន តាមទិសដៅនៃលំហវ៉ិចទ័រ $\vect{\E}$។
- គេហៅ ចំណុចមានទម្ងន់ ក្នុងលំហអាហ្វីន $\mathcal{E}$ គឺគ្រប់គូ $(A,\alpha)$ ដែល $A\in \mathcal{E}$ និង $\alpha\in \mathbb{R}$ ។ ក្នុងករណីនេះ $\alpha$ ហៅថា ទម្ងន់ ឬក៏ ម៉ាស របស់ចំណុច $A\in\calE$។
- បើ $\big\{(A_{i}, \alpha_{i})\big\}_{i=1}^{m}$ ជាប្រព័ន្ធនៃចំណុចមានទម្ងន់របស់លំហអាហ្វីន $\mathcal{E}$ នោះ $\alpha = \sum_{i=1}^{m} \alpha_{i}$ ហៅថា ម៉ាសសរុប។
យក $\mathcal{E}$ ជាលំហអាហ្វីនតាមទិសដៅ $\vect{\E}$ និងយក $\bigg\{(A_{1},\alpha_{1})$, $(A_{2},\alpha_{2})$, $\ldots$, $(A_{m}, \alpha_{m})\bigg\}$ ជាប្រព័ន្ធចំណុចមានទម្ងន់របស់លំហ $\calE$។ គេកំណត់ អនុគមន៍វ៉ិចទ័រ Leibnitz ដូចខាងក្រោម៖ \[ \begin{array}{rcl} \varphi:\mathcal{E} &\longrightarrow & \vect\E\\ M &\longmapsto & \varphi(M) = \displaystyle\sum_{i=1}^{m}\alpha_{i}\,\vect{MA_{i}} \end{array} \] ដូច្នេះ គេបាន
- បើ $ \sum_{i=1}^{m}\alpha_{i} = 0$ នោះ $\varphi$ ជាអនុគមន៍ថេរ
- បើ $ \sum_{i=1}^{m}\alpha_{i}\neq 0$ នោះ $ \varphi$ ជាអនុវត្តន៍មួយទល់មួយ។
និយមន័យ និងលក្ខណៈរបស់បារីសង់
គេកំណត់ $\big\{(A_{i}, \alpha_{i})\big\}_{i=1}^{m}$ ជាចំណុចមានទម្ងន់របស់លំហអាហ្វីន $\mathcal{E}$ តាមទិសដៅនៃវ៉ិចទ័រ $\vect{\E}$ ដែល $ \sum_{i=1}^{m}\alpha_{i}\neq 0 $ ។ គេហៅ បារីសង់នៃប្រព័ន្ធចំណុច $\big\{(A_{i}, \alpha_{i})\big\}_{i=1}^{m}$ គឺជាចំណុច $G$ តែមួយគត់នៃលំហ $\mathcal{E}$ ដែលកំណត់ដោយ $$ \sum_{i=1}^{m} \alpha_{i}\vect{GA_{i}} = \vect{0} $$
តាមនិយមន័យខាងលើ គេកំណត់សរសេរ \[ \fcolorbox{Red}{blue!5}{\quad $\displaystyle\operatorname{Bar}\big\{(A_{i}, \alpha_{i})\big\} = G\in\calE \Longleftrightarrow \sum_{i=1}^{m} \alpha_{i}\,\vect{GA_{i}} = \vect{0} $\quad } \]
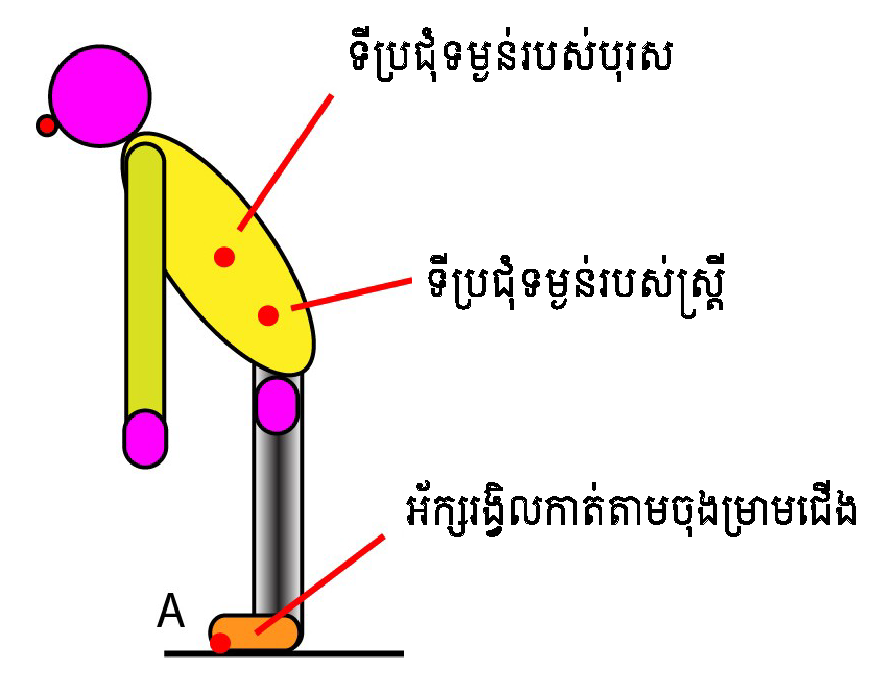
Fig.2: ទីប្រជុំទំងន់របស់មនុស្សប្រុស និងស្រី ។
សំគាល់: គេបានលក្ខណៈសំខាន់ៗរបស់បារីសង់ដូចខាងក្រោម៖
- យក $G$ ជាបារីសង់នៃប្រព័ន្ធចំណុចមានទម្ងន់ $\big\{(A_{i}, \alpha_{i})\big\}_{i=1}^{m}$ ។ ដូច្នេះ ចំពោះគ្រប់ចំណុច $A\in \mathcal{E}$ គេបាន $$ \vect{AG} = \frac{1}{\alpha} \sum_{i=1}^{m} \alpha_{i}\vect{AA_{i}}\quad \text{ where } \ \ \alpha = \sum_{i=1}^{m}\alpha_{i} $$
- បើ $\alpha_{1}=\alpha_{2}=\cdots=\alpha_{m}=1$ នោះគេថា $G$ គឺជា អ៊ីសូបារីសង់ នៃចំណុច $A_{1},A_{2}, \ldots, A_{m}$។ ក្នុងករណីនេះ ចំពោះគ្រប់ចំណុច $A\in \mathcal{E}$ គេបាន $$ \vect{AG} = \frac{1}{m}\sum_{i=1}^{m} \vect{AA_{i}} $$
- ចំពោះគ្រប់ $\lambda\in \mathbb{R}^{*}$ នោះគេបាន ប្រព័ន្ធចំណុចមានទម្ងន់ $\big\{(A_{i}, \alpha_{i})\big\}_{i=1}^{m}$ និង $\big\{(A_{i}, \lambda\;\alpha_{i})\big\}_{i=1}^{m}$ មានបារីសង់ដូចគ្នា។
យក $\mathcal{E}$ ជាលំហអាហ្វីនកំណត់តាមទិសដៅនៃលំហ $\vect{\E}$។ កំណត់ $A$ និង $B$ ជាចំណុចពីរផ្សេងគ្នារបស់លំហ $\mathcal{E}$។ សំណុំបារីសង់ នៃចំណុចមានទម្ងន់ $(A, \alpha)$ និង $(B,\beta)$ ដែលមាន $\alpha\geq 0$ និង $\beta\geq 0$ មានឈ្មោះថា អង្កត់ ដែលភ្ជាប់ចំណុច $A$ និង $B$ ដែលតាងដោយ $[A,B]$។ ដូច្នេះ គេបាន $$\fbox{$ M \in[A,B] \Longleftrightarrow \exists\ (\alpha,\beta)\in \mathbb{R}_{+}^{2}:\ \alpha +\beta \neq 0\ \text{ and } \ \alpha\cdot\vect{MA} + \beta\cdot\vect{MB} = \vect{0}$} $$ ដោយគ្រប់ $\lambda\in \mathbb{R}^{*}$ គេបានចំណុច $(A,\alpha)$ និង $(B,\beta)$ មានបារីសង់ដូចគ្នានឹងចំណុច $(A,\lambda\alpha)$ និង $(B, \lambda\beta)$ ដែរ។ ដូច្នេះ ដោយសន្មត់យក $\lambda = \dfrac{1}{\alpha+\beta}$ នោះគេបាន \begin{eqnarray*} M\in[A,B] &\Longleftrightarrow & \exists\ (\alpha,\beta)\in \mathbb{R}_{+}^{2}:\ \alpha +\beta = 1\ \text{ and }\ \alpha\vect{MA} + \beta \vect{MB} = \vect{0}\\ &\Longleftrightarrow & \exists\ \alpha\in[0,1]:\ \alpha\cdot\vect{MA} + (1-\alpha)\vect{MB} = \vect{0}\\ &\Longleftrightarrow & \exists\ \alpha\in[0,1]:\ \vect{AM}= (1-\alpha)\vect{AB} \end{eqnarray*} ជាពិសេស ចំណុចកណ្ដាល $I$ នៃអង្កត់ $[A,B]$ ត្រូវបានកំណត់ដោយ៖ \begin{eqnarray*} I \text{ midpoint of } [A,B] &\Longleftrightarrow & \vect{IA} + \vect{IB} = \vect 0\\ &\Longleftrightarrow & \forall O \in\mathcal{E}, \ \vect{OI} = \frac{1}{2}\left(\vect{OA} + \vect{OB}\right)\\ &\Longleftrightarrow & \vect{AI} = \frac{1}{2} \vect{AB} \end{eqnarray*}
ឧបមាយក $A, B$ និង $C$ ជាបីចំណុចរត់មិនត្រង់គ្នារបស់លំហ $\mathcal{E}$។ ដូច្នេះ ចំណុច $A, B$ និង $C$ បង្កើតបានជា ត្រីកោណមួយ ដែលតាងដោយ $\triangle ABC$ ឬ $(ABC)$ ដែលមានអង្កត់ $[A,B], [A,C]$ និង $[B,C]$ ហៅថា ជ្រុង របស់ត្រីកោណនេះ។ អ៊ីសូបារីសង់ $G$ នៃចំណុច $A, B$ និង $C$ ហៅថា ទីប្រជុំទម្ងន់ របស់ត្រីកោណ $ABC$ ដែលកំណត់ដោយ $$ \vect{GA}+\vect{GB}+\vect{GC} = \vect{0} $$ ដូច្នេះ បើ $G$ ជាបារីសង់របស់ត្រីកោណ $ABC$ នោះគេបាន \begin{gather*} \vect{AG} = \frac{1}{3}\left(\vect{AB} + \vect{AC}\right)\\ \vect{BG} = \frac{1}{3}\left(\vect{BA}+\vect{BC}\right)\\ \vect{CG} = \frac{1}{3}\left(\vect{CA}+\vect{CB}\right) \end{gather*}
គេហៅ មេដ្យាន ដែលគូសចេញពីចំណុច $A$ នៃត្រីកោណ $ABC$ គឺជាបន្ទាត់ $(AI)$ ដែលកាត់តាមចំណុច $A$ និងចំណុច $I$ កណ្ដាល $[B,C]$។
Remark: ត្រីកោណមួយមានមេដ្យានចំនួនបី គឺ៖ $(AI), (BJ)$ និង $(CK)$ ដែល $I, J$ និង $K$ គឺជាចំណុចកណ្ដាលរៀងគ្នានៃអង្កត់ $[B,C], [A,C]$ និង $[A,B]$។
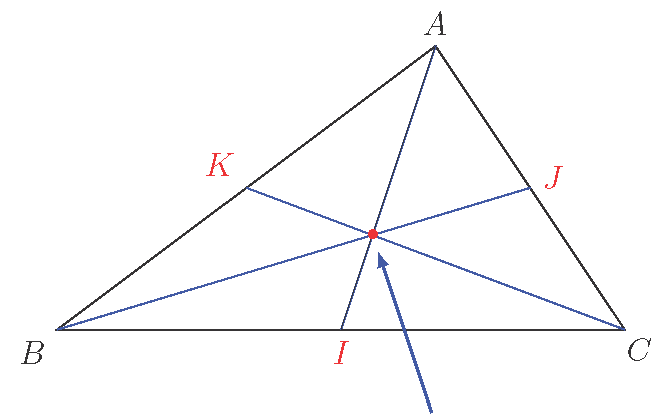
Fig.3: ទីប្រជុំទម្ងន់របស់ត្រីកោណ $ABC$
មេដ្យានទាំងបីរបស់ត្រីកោណ $ABC$ ប្រសព្វគ្នាត្រង់ចំណុចកណ្ដាលនៃទីប្រជុំទម្ងន់ $G$ របស់ត្រីកោណនេះ។ គេបាន $$ \vect{AG} = \frac{2}{3}\vect{AI},\quad \vect{BG} = \frac{2}{3}\vect{BJ}\quad \text{ and }\quad \vect{CG} = \frac{2}{3}\vect{CK} $$ ដែល $I, J$ និង $K$ ជាចំណុចកណ្ដាលរៀងគ្នានៃអង្កត់ $[B,C], [A,C]$ និង $[A,B]$។
Proof: ដោយយក $I, J$ និង $K$ ជាចំណុចកណ្ដាលរៀងគ្នានៃអង្កត់ $[B,C], [A,C]$ និង $[A,B]$ នោះគេបាន $$ \vect{AI} = \frac{1}{2}\left(\vect{AB}+\vect{AC}\right), \quad \vect{BJ} = \frac{1}{2}\left(\vect{BA}+\vect{BC}\right), \quad \vect{CK} = \frac{1}{2}\left(\vect{CA}+\vect{CB}\right) $$ ដូច្នេះ $\vect{AG} = \dfrac{1}{3}\left(\vect{AB}+\vect{AC}\right) = \dfrac{2}{3}\vect{AI}$ ។ ដូច្នេះ គេបាន $G\in(AI)$។ តាមលក្ខណៈដូចគ្នានេះ គេអាចបង្ហាញថា $\vect{BG} = \frac{2}{3}\vect{BJ} {\text{, }} \vect{CG} = \frac{2}{3}\vect{CK} $ ។ ដូច្នេះ $G\in(AI)\cap (BJ) \cap (CK)$ ។
-
Let points $M, N$ and $P$ in a plane $\mathcal P$ with a frame (តម្រុយ) $(O, \vec{\imath}, \vec{\jmath})$. The coordinates of $M, N$ and $P$ are $(2,3),(6,4)$ and $\left(-6,-\frac{1}{2}\right)$ respectively. Show that
$$
\left|\begin{array}{ccc}
2 & 6 & -6 \\
3 & 4 & -\frac{1}{2} \\
1 & 1 & 1
\end{array}\right|\neq 0, \qquad \tag{1}
$$
How can you say from relation $(1)$ that the three points are colinear?
Now, let $\left(x_{A}, y_{A}\right)$ and $\left(x_{B}, y_{B}\right)$ be the coordinates of $A$ and $B$. Show that the equation of the line $(AB)$ is givent by $$ \left|\begin{array}{ccc} x & x_{A} & x_{B} \\ y & y_{A} & y_{B} \\ 1 & 1 & 1 \end{array}\right|=0 $$ -
Let $\mathcal E = \mathbb R^3$ be an affine space with a frame $(O, \vec{\imath}, \vec{\jmath}, \vec{k})$ which is not orthonormal.
- Let $M, N$ and $P$ be points in $\mathcal P$ with coordinates $(4,0,0),(0,5,0)$ and $(0,0,6)$ respectively. Find the equation of the plane $\mathcal P = \mathbf{Aff}\Big(\{M, N, P\}\Big)$.
- Find the coordinates of the barycentre $G$ of the triangle $MNP$. Verify that $G$ belongs to the plane $\mathcal P$.
-
Let $A, B$ and $C$ be three points in a plane $\mathcal P$ and let $\gamma \in[0,1]$. Let
- $D(\gamma)$ be the barycenter of $A$ and $B$ with the masses $(1-\gamma)$ and $\gamma$;
- $E(\gamma)$ be the barycenter of $B$ and $C$ with the masses $(1-\gamma)$ and $\gamma$ and
- $F(\gamma)$ be the barycenter of $D(\gamma)$ and $E(\gamma)$ with the masses $(1-\gamma)$ and $\gamma$.
-
Let $E$ be the ordinary space of geometry with $(O, \vec{\imath}, \vec{\jmath}, \vec{k})$ be a frame $E$. We suppose that $E$ is euclidean and that the frame $(O, \vec{\imath}, \vec{\jmath}, \vec{k})$ is orthonormal.
- Let $X$ be a point with coordinates $(2,-10,3)$ and let $\vec{u}$ be the vector $\vec{u}=3 \vec{\imath}+\frac{12}{5} \vec{\jmath}+2 \vec{k}$. Write the equation of the plane $\mathcal P$ which contains $X$ and is orthogonal to $\vec{u}$.
- Let $A, B$ and $C$ be the points of intersection of $\mathcal P$ with the axis $O x, O y$ and $O z$. Find the coordinates of the points $A, B$ and $C$.
- Compute the coordinates of the barycentre of the triangle $A B C$
- Draw a picture showing the points $X, A, B$ and $C$ and the vector $\vec{u}$.
- Check that the vectors $\overrightarrow{X A}, \overrightarrow{X B}$ and $\overrightarrow{X C}$ are orthogonal to $\vec{u}$.
លំហអាហ្វីនមានវិមាត្ររាប់អស់
តម្រុយអាហ្វីន - កូអរដោនេនៃបារីសង់
យក $\mathcal{E}$ គឺជាលំហអាហ្វីនតាមទិសដៅនៃលំហ $\vect{\E}$។ យក $A_{0},A_{1}, \ldots, A_{m}$ ជាចំណុចរបស់លំហ $\mathcal{E}$។ គេថា ប្រព័ន្ធ $\{A_{0},A_{1},\ldots,A_{m}\}$ គឺជាប្រព័ន្ធមិនអាស្រ័យលីនេអ៊ែរតាមលក្ខណៈអាហ្វីន បើប្រព័ន្ធ $$\bigg\{\vect{A_{0}A_{1}},\vect{A_{0}A_{2}}, \ldots,\vect{A_{0}A_{m}}\bigg\}$$ មិនអាស្រ័យលីនេអ៊ែរ។
ពិនិត្យឧទាហរណ៍ខាងក្រោម៖
- បើ $A$ និង $B$ ជាចំណុចពីរផ្សេងគ្នារបស់ $\mathcal{E}$ នោះគេបាន $\{A,B\}$ គឺជាប្រព័ន្ធមិនអាស្រ័យលីនេអ៊ែរតាមន័យអាហ្វីន, i.e. $\bigg\{\vect{AB}\bigg\}$ l.i ។
- បើ $A, B$ និង $C$ គឺជាចំណុចបីរត់មិនត្រង់គ្នា នោះប្រព័ន្ធ $\{A,B,C\}$ គឺជាប្រព័ន្ធមិនអាស្រ័យលីនេអ៊ែរតាមន័យអាហ្វីន i.e. $\bigg\{\vect{AB}, \vect{AC}\bigg\}$ l.i ។
-
បើគេមានបួនចំណុច $A, B, C$ និង $D$ មិនអាស្រ័យលីនេអ៊ែរគ្នាតាមន័យអាហ្វីន នោះគេបង្កើតបាន តេត្រាអែត មួយ។

Fig.4: តេត្រាអែត
យក $\mathcal{E}$ ជាលំហអាហ្វីនតាមទិសដៅនៃវ៉ិចទ័រ $\vect{\E}$។ គេហៅ តម្រុយអាហ្វីន (affine frame) របស់លំហ $\mathcal{E}$ គឺជាប្រព័ន្ធចំណុច $\Big\{A_{0}, A_{1},\ldots, A_{m}\Big\}$ របស់ $\mathcal{E}$ ដែលផ្ទៀងផ្ទាត់លក្ខខណ្ឌដូចតទៅ៖
- $\mathcal{E} = {\bf Aff}\Big(\big\{A_{0},A_{1}, \cdots, A_{m}\big\}\Big)$
- $\big\{A_{0},A_{1}, \ldots, A_{m}\big\}$ មិនអាស្រ័យលីនេអ៊ែរតាមន័យអាហ្វីន។
- បើ $A$ និង $B$ ជាចំណុចពីរផ្សេងគ្នា នោះគេបាន $\big(A,B\big)$ គឺជាតម្រុយអាហ្វីនរបស់បន្ទាត់អាហ្វីន $(AB)$ ដែលកាត់តាមចំណុច $A$ និង $B$។
- បើ $A, B$ និង $C$ ជាចំណុចបីរត់មិនត្រង់គ្នា គេបាន $\big(A,B,C\big)$ គឺជាតម្រុយអាហ្វីនរបស់ប្លង់អាហ្វីន $(ABC)$ ដែលកាត់តាមចំណុច $A, B$ និង $C$។
យក $\mathcal{E}$ គឺជាប្លង់អាហ្វីនតាមទិសដៅនៃលំហ $\vect{\E}$ និងមានវិមាត្រស្មើ $n$។ គេបាន $\vect{\E}$ មានតម្រុយអាហ្វីនយ៉ាងតិចមួយ។
Proof: យក $\Big\{\vect{e_{1}}, \vect{e_{2}},\ldots,\vect{e_{n}}\Big\}$ គឺជាគោលមួយរបស់លំហ $\vect{\E}$។ ដោយកំណត់ចំណុចមួយ $A_{0}\in \mathcal{E}$ នោះចំពោះគ្រប់ $i\in\{1,2, \ldots ,n\}$ មានចំណុចតែមួយគត់ $A_{i}\in \mathcal{E}$ ដែល $\vect{A_{0}A_{i}} = \vect{e_{i}}$។
ជាការពិត គេបង្ហាញបានយ៉ាងងាយថា $$\mathcal{E} = {\bf Aff}\Big(\big\{A_{0},A_{1}, \ldots, A_{n}\big\}\Big) \quad\text{and}\quad \Big\{A_{0},A_{1}, \ldots,A_{n}\Big\} - \text{ l.i}$$ តាមន័យអាហ្វីន។
កូអរដោនេបារីសង់
យក $\mathcal{E}$ ជាលំហអាហ្វីនមានវិមាត្រស្មើ $n$ និងកំណត់ $\Big\{A_{0},A_{1}, \ldots,A_{n}\Big\}$ ជាតម្រុយអាហ្វីនរបស់លំហ $\mathcal{E}$។ ដូច្នេះ ចំពោះគ្រប់ $M\in \mathcal{E}$ គេកំណត់បាន $n+1$-ធាតុ $(\alpha_{0},\alpha_{1},\ldots,\alpha_{n})\in \mathbb{R}^{n+1}$ តែមួយគត់ ដែល $ \alpha_{0}+\alpha_{1}+\cdots+\alpha_{n}=1 $ និង \[ \sum_{i=0}^{n}\alpha_{i}\vect{MA_{i}}=\vect{0} \] ក្នុងករណីនេះ $\alpha_{0}, \alpha_{1}, \ldots, \alpha_{n}$ ហៅថា កូអរដោនេបារីសង់ របស់ចំណុច $M$ នៅក្នុងតម្រុយអាហ្វីន $\Big(A_{0},A_{1},\ \ldots,A_{n}\Big)$ ។
Proof:
គេកំណត់ $\Big\{A_{0},A_{1},\ldots,A_{n}\Big\}$ មិនអាស្រ័យលីនេអ៊ែរតាមន័យអាហ្វីន។ តាមនិយមន័យ គេបាន $\Big\{\vect{A_{0}A_{1}},\vect{A_{0}A_{2}},\ldots,\vect{A_{0}A_{n}}\Big\}$ មិនអាស្រ័យលីនេអ៊ែរនៅក្នុងលំហ $\vect{\E}$ ឬបើ $\dim(E)=n$ នោះគេបាន $\Big\{\vect{A_{0}A_{1}},\vect{A_{0}A_{2}}, \ldots,\vect{A_{0}A_{m}}\Big\}$ គឺជាគោលមួយរបស់ $\vect{\E}$។
ដោយ $M\in \mathcal{E}$ នោះមានធាតុតែមួយគត់ $(\beta_{1},\beta_{2}, \ldots, \beta_{n})\in \mathbb{R}^{n}$ ដែល
$$
\vect{A_{0}M}=\sum_{i=1}^{n}\beta_{i}\vect{A_{0}A_{i}}
$$
គេបាន
\begin{eqnarray*}
\vect{A_{0}M} = \sum_{i=1}^{n}\beta_{i}\vect{A_{0}A_{i}}\ &\Longrightarrow & \vect{A_{0}M} = \sum_{i=1}^{n}\beta_{i}\left(\vect{MA_{i}}-\vect{MA_{0}}\right)\\
&\Longrightarrow & \vect{MA_{0}}+\sum_{i=1}^{n}\beta_{i}\vect{MA_{i}} - \sum_{i=1}^{n}\beta_{i}\vect{MA_{0}} = \vect{0} \\
&\Longrightarrow & \left(1-\sum_{i=1}^{n}\beta_{i}\right)\vect{MA_{0}} + \sum_{i=1}^{n}\beta_{i}\vect{MA_{i}} = \vect{0}
\end{eqnarray*}
ដោយតាង $\displaystyle \alpha_{0} = 1-\sum_{i=1}^{n}\beta_{i}$ និង $\forall i\in\{1,2,\ldots,n\},\ \alpha_{i}=\beta_{i}$ នោះគេបាន
$$
\sum_{i=0}^{n}\alpha_{i}=1\quad \text{ and } \quad \sum_{i=0}^{n}\alpha_{i}\vect{MA_{i}} = \vect{0}
$$
ដែលគេកំណត់បានអត្ថិភាពរបស់ $\alpha_{0}, \alpha_{1}, \ldots, \alpha_{n}$។ ចំពោះភាពមានតែមួយគត់ គេត្រូវសន្មត់ថា មានធាតុ $\lambda_{0}, \lambda_{1}, \ldots, \lambda_{n}$ ដែលផ្ទៀងផ្ទាត់លក្ខណៈដូចគ្នាទៅនឹង $\alpha_{0}, \alpha_{1}, \ldots , \alpha_{n}$ ដែរ។ ដូច្នេះ គេបាន
$$
\vect{A_{0}M} = \sum_{i=1}^{n}\alpha_{i}\vect{A_{0}A_{i}}\quad \text{ and } \quad \vect{A_{0}M}=\sum_{i=1}^{n}\lambda_{i}\vect{A_{0}A_{i}}
$$
ដូច្នេះ $\forall i\in\{1,2,\ldots,\ n\}, \alpha_{i}=\lambda_{i}$ និងដោយសារតែ
$$
\sum_{i=0}^{n}\alpha_{i} = \sum_{i=0}^{n}\lambda_{i}=1
$$
នោះគេទទួលបាន $\alpha_{0}=\lambda_{0}$។
REMARK: បើ $\Big(A_{0},A_{1},\ldots,A_{n}\Big)$ ជាតម្រុយអាហ្វីនមួយលើ $\mathcal{E}$ នោះចំពោះគ្រប់ចំណុច $M\in \mathcal{E}$ មានធាតុតែមួយគត់ $(\alpha_{0},\alpha_{1},\ldots, \alpha_{n})\in \mathbb{R}^{n+1}$ ដែល $\alpha_{0}+\alpha_{1}+\cdots+\alpha_{n}=1$ ហើយ $M$ គឺជាបារីសង់នៃចំណុចទាំងឡាយមានទម្ងន់ $(A_{0}, \alpha_{0}) , (A_{1}, \alpha_{1}) , \ldots,\ (A_{n},\alpha_{n})$។
អនុវត្តន៍មួយចំនួនទាក់ទងនឹងកូអរដោនេបារីសង់
យក $\mathcal{E}$ គឺជាប្លង់អាហ្វីនកំណត់តាមទិសដៅនៃលំហ $\vect{\E}$ ដែលមានតម្រុយអាហ្វីន $\big\{A,B,C\big\}$ និងកំណត់ $M, N$ និង $P$ គឺជាចំណុចបីរបស់លំហ $\mathcal{E}$ ដែលមានកូអរដោនេបារីសង់ រៀងគ្នាគឺ $(\alpha, \beta,\gamma),\ (\alpha', \beta',\gamma')$ និង $(\alpha'', \beta'', \gamma'')$ កំណត់ក្នុងតម្រុយ $\big\{A,B,C\big\}$ នេះ។ ដូច្នេះ គេបាន $M, N$ និង $P$ ជាចំណុចបីរត់ត្រង់គ្នា លុះត្រាតែ $$ \left|\begin{array}{lll} \alpha & \alpha' & \alpha''\\ \beta & \beta' & \beta''\\ \gamma & \gamma' & \gamma'' \end{array}\right| = 0 $$
Proof:
ករណីចាំបាច់៖ ដោយ $\alpha+\beta+\gamma = \alpha'+\beta'+\gamma' = \alpha''+\beta''+\gamma''=1$ នោះគេបាន
\begin{eqnarray*}
\begin{vmatrix}
\alpha & \alpha' & \alpha''\\
\beta & \beta' & \beta''\\
\gamma & \gamma' & \gamma''
\end{vmatrix} = \begin{vmatrix}
1& 1 & 1\\
\beta & \beta' & \beta''\\
\gamma & \gamma' & \gamma''
\end{vmatrix}
&=& \begin{vmatrix}
1 & 0 & 0\\
\beta & \beta'-\beta & \beta''-\beta\\
\gamma & \gamma'-\gamma & \gamma''-\gamma
\end{vmatrix} \\
&=&
\begin{vmatrix}
\beta'-\beta & \beta''-\beta\\
\gamma'-\gamma & \gamma''-\gamma
\end{vmatrix}
\end{eqnarray*}
ម្យ៉ាងទៀត គេបាន
\begin{eqnarray*}
\vect{AM} &=& \beta\vect{AB}+\gamma \vect{AC}\\
\vect{AN} &=& \beta'\vect{AB}+\gamma'\vect{AC}\\
\vect{AP} &=& \beta''\vect{AB}+\gamma''\vect{AC}
\end{eqnarray*}
ដូច្នេះ
\begin{eqnarray*}
\vect{MN} &=& (\beta'-\beta)\vect{AB} + (\gamma' -\gamma)\vect{AC}\\
\vect{MP} &=& (\beta''-\beta)\vect{AB} + (\gamma''-\gamma)\vect{AC}
\end{eqnarray*}
ករណីគ្រប់គ្រាន់៖ គេដឹងថា $M, N$ និង $P$ ជាបីចំណុចរត់ត្រង់គ្នា លុះត្រាតែ $\left\{\vect{MN},\vect{MP}\right\}$ អាស្រ័យលីនេអ៊ែរគ្នា។
ដោយ $\Big\{\vect{AB},\vect{AC}\Big\}$ គឺជាគោលមួយរបស់ $\vect{\E}$ ។ ដូច្នេះគេបាន៖ \begin{eqnarray*} \Big\{\vect{MN},\vect{MP}\Big\}\ \text{ l.d } &\Longleftrightarrow & \det\Big(\vect{MN},\vect{MP}\Big) = 0\\ &\Longleftrightarrow& \begin{vmatrix} \beta'-\beta & \beta''-\beta\\ \gamma'-\gamma & \gamma''-\gamma \end{vmatrix}=0 \end{eqnarray*}
ដូច្នេះ គេទទួលបានចម្លើយ។ឧបមាថា $\mathcal{E}$ ជាប្លង់អាហ្វីន។ គេកំណត់ $ABC$ ជាត្រីកោណមួយ និងយកបីចំណុច $P, Q$ និង $R$ របស់ប្លង់អាហ្វីន $\mathcal{E}$ ដែលផ្ទៀងផ្ទាត់ $P\in(AB), Q\in(BC)$ និង $R\in(AC)$ ដោយគេដឹងថា $P\not\in\{A,B\}, Q\not\in\{B,C\}$ និង $R\not\in\{A,C\}$។ ហើយគេសន្មត់ $\vect{PA} = \alpha\ \vect{PB},\ \vect{QB} = \beta\ \vect{QC}$ និង $\vect{RC} = \gamma\ \vect{RA}$។ ដូច្នេះ បីចំណុច $P, Q$ និង $R$ រត់ត្រង់គ្នា លុះត្រាតែ $\alpha\beta\gamma=1$។
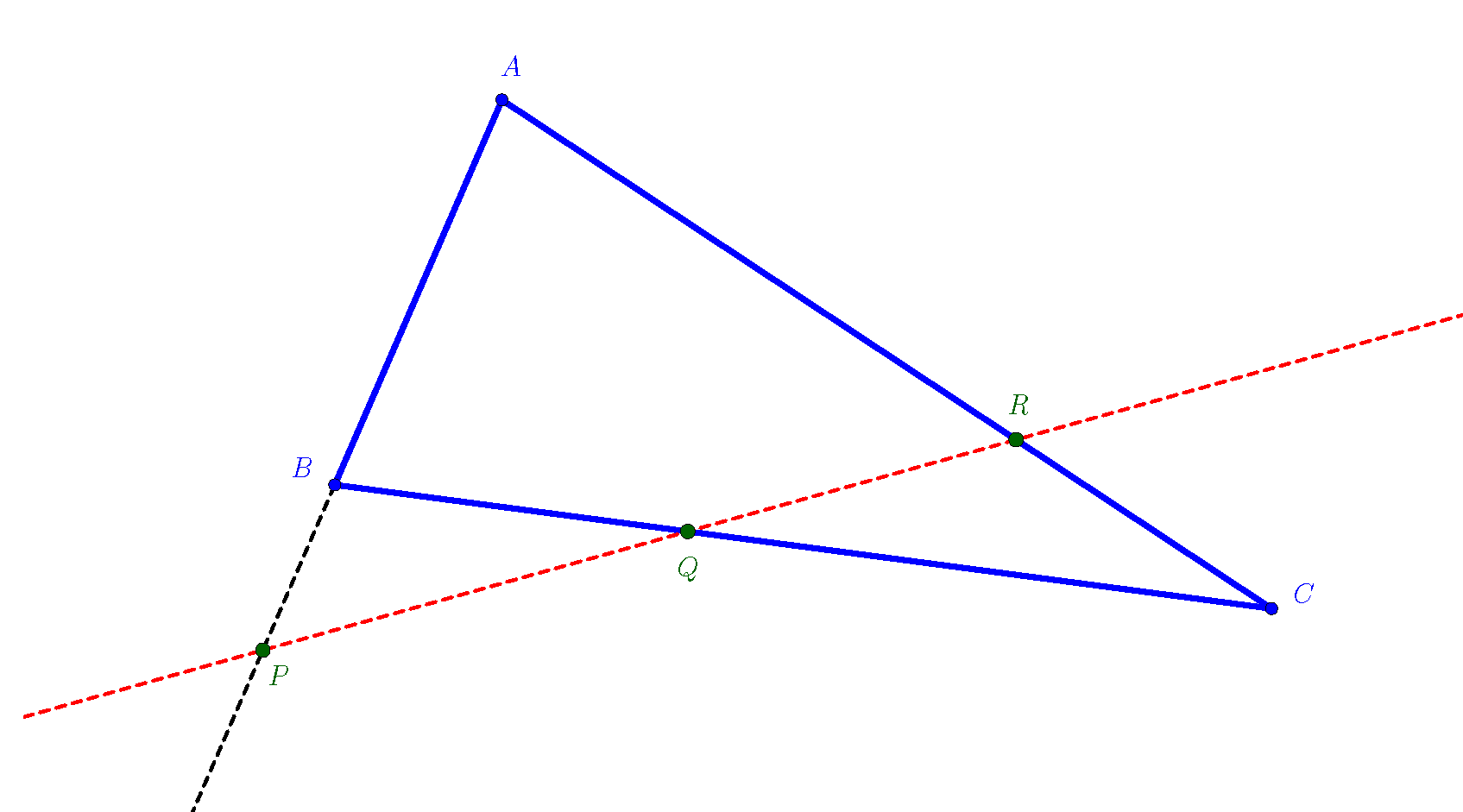
Fig.5: ទ្រឹស្ដីបទ Menelaus: $P, Q$ និង $R$ ជាបីចំណុចរត់ត្រង់គ្នា
Proof: ដោយ $\mathcal{E}$ គឺជាប្លង់អាហ្វីន ហើយ $A, B, C$ គឺជាបីចំណុចរត់មិនត្រង់គ្នា នោះគេបាន $(A,B,C)$ គឺជាតម្រុយអាហ្វីនមួយលើ $\mathcal{E}$។ ដូច្នេះ \begin{eqnarray*} P \text{ with }:\quad &&\left(\displaystyle \frac{1}{1-\alpha}, \frac{-\alpha}{1-\alpha},0\right)\\ Q \text{ with }:\quad &&\left(0,\displaystyle \ \frac{1}{1-\beta},\frac{-\beta}{1-\beta}\right) \quad \\ R \text{ with }:\quad &&\left(\displaystyle \frac{-\gamma}{1-\gamma},0,\ \frac{1}{1-\gamma}\right) \end{eqnarray*} ដូច្នេះ តាមសំណើខាងលើ គេបាន \begin{eqnarray*} P, Q, R \ {\text{ aligned }} &\Longleftrightarrow & \begin{vmatrix} 1 & 0 & -\gamma\\ -\alpha & 1 & 0\\ 0 & -\beta & 1 \end{vmatrix} = 0 \\ &\Longleftrightarrow & 1-\gamma\alpha\beta = 0\\ &\Longleftrightarrow & \alpha\beta\gamma = 1 \end{eqnarray*}
តម្រុយដេកាត $-$ កូអរដោនេដេកាត
យក $\mathcal{E}$ ជាលំហអាហ្វីនកំណត់តាមទិសដៅនៃលំហ $\vect{\E}$ និងមានវិមាត្រ $n$។ គេហៅ តម្រុយដេកាត (Cartesian frame) របស់លំហ $\mathcal{E}$ គឺជាប្រព័ន្ធ $\big(\Omega, \vect{e_{1}}, \vect{e_{2}}, \ldots, \vect{e_{n}}\big)$ ដែល $\Omega$ ហៅថា គល់តម្រុយ គឺជាចំណុចទូទៅរបស់លំហ $\mathcal{E}$ ហើយ $\big\{\vect{e_{1}}, \vect{e_{2}}, \ldots, \vect{e_{n}}\big\}$ គឺជាគោលទូទៅមួយរបស់លំហ $\vect{\E}$។
REMEMBER: បើប្រព័ន្ធ $\Big(A_{0},A_{1},A_{2},\ldots,A_{n}\Big)$ គឺជាតម្រុយអាហ្វីនរបស់លំហ $\mathcal{E}$ នោះគេបាន $$\Big(A_{0},\vect{A_{0}A_{1}},\vect{A_{0}A_{2}},\ldots,\vect{A_{0}A_{n}}\Big)$$ គឺជាតម្រុយដេកាតរបស់លំហ $\mathcal{E}$។
- បើ $A$ និង $B$ គឺជាចំណុចពីរផ្សេងគ្នារបស់លំហ $\mathcal{E}$ នោះគេបាន $\Big(A,\vect{AB}\Big)$ គឺជាតម្រុយដេកាតរបស់បន្ទាត់អាហ្វីន ដែលកាត់តាមចំណុច $A$ និង $B$។
- បើ $A, B$ និង $C$ គឺជាចំណុចបីរត់មិនត្រង់គ្នារបស់លំហ $\mathcal{E}$ នោះគេបាន $\Big(A,\vect{AB},\vect{AC}\Big)$ គឺជាតម្រុយដេកាតរបស់ប្លង់អាហ្វីន ដែលកាត់តាមចំណុច $A, B$ និង $C$។
យក $\mathcal{E}$ គឺជាលំហអាហ្វីនមានវិមាត្រ $n$ មានតម្រុយដេកាត $\Big(\Omega,\vect{e_{1}}, \vect{e_{2}}, \ldots,\vect{e_{n}}\Big)$។ ដូច្នេះ ចំពោះគ្រប់ចំណុច $M\in \mathcal{E}$ នោះមានធាតុតែមួយគត់ $\big(x_{1},x_{2},\ldots,x_{n}\big)\in \mathbb{R}^{n}$ ដែល $$ \vect{\Omega M}=\sum_{i=1}^{n}x_{i}\vect{e_{i}} $$ ក្នុងករណីនេះ $x_{1},x_{2}, \ldots, x_{n}$ ហៅថា កូអរដោនេដេកាត របស់ចំណុច $M$ ធៀបទៅនឹងតម្រុយដេកាត $\Big(\Omega, \vect{e_{1}}, \vect{e_{2}}, \ldots, \vect{e_{n}}\Big)$។
សមីការទម្រង់ប៉ារ៉ាម៉ែត្រតាងលំហអាហ្វីនរង
យក $\mathcal{E}$ ជាលំហអាហ្វីនមានវិមាត្រ $n$ ដែលប្រដាប់ដោយតម្រុយដេកាត $\Big(O,\vect{e_{1}},\vect{e_{2}}, \ldots, \vect{e_{n}}\Big)$។ កំណត់ $\mathcal{F}$ ជាលំហអាហ្វីនរងរបស់ $\mathcal{E}$ ដែលកាត់តាមចំណុច $A$ មានកូអរដោនេ $(a_{1},a_{2},\ldots,a_{n})$ តាមទិសដៅ $\vect\F$ ដែល $\dim(\vect\F)=p$។ យក $\Big\{\vect{v}_1, \vect{v}_2, \ldots, \vect{v}_p\Big\}$ ជាគោលមួយរបស់លំហរង $F$ ដូច្នេះ គេបាន ៖ $$ \forall j\in\{1, 2, \cdots,p\},\quad \vect{v_{j}}=\sum_{i=1}^{n}\alpha_{ij}\vect{e_{i}} $$
ដោយយក $M$ ជាចំណុចមួយទូទៅរបស់ $\mathcal{E}$ មានកូអរដោនេ $\big(x_{1},x_{2}, \ldots,x_{n}\big)$ នោះគេបាន \begin{eqnarray*} M\in \mathcal{F} &\Longleftrightarrow & \vect{AM}\in \vect\F\\ &\Longleftrightarrow & \exists\ (\lambda_{1},\lambda_{2}, \ldots,\lambda_{p})\in \mathbb{R}^{p}:\ \vect{AM}=\sum_{j=1}^{p}\lambda_{j}\vect{v_{j}}\\ &\Longleftrightarrow & \exists\ (\lambda_{1},\lambda_{2},\ \ldots,\lambda_{p})\in \mathbb{R}^{p}:\ \vect{AM}=\sum_{i=1}^{n}\left(\sum_{j=1}^{p}\lambda_{j}\alpha_{ij}\right)\vect{e_{i}}\\ &\Longleftrightarrow & \exists\ (\lambda_{1},\lambda_{2},\ \ldots,\lambda_{p})\in \mathbb{R}^{p}:\ \fbox{$\displaystyle\vect{OM}=\sum_{i=1}^{n}\left(\sum_{j=1}^{p}\lambda_{j}\alpha_{ij}\right)\vect{e_{i}}+\vect{OA}$} \end{eqnarray*} ដូច្នេះ គេទទួលបានប្រព័ន្ធមួយខាងក្រោម ហៅថា សមីការប៉ារ៉ាម៉ែត្រ របស់លំហអាហ្វីនរង $\mathcal{F}$ ៖ $$\fbox{$\begin{gather*} M\in \mathcal{F} \Longleftrightarrow \exists\ (\lambda_{1},\lambda_{2},\ \ldots,\lambda_{p})\in \mathbb{R}^{p}\ \text{ s.t } \\ %\left\{ \begin{array}{lcl} x_{i} &=&\displaystyle\sum_{j=1}^{p}\lambda_{j}\alpha_{ij}+a_{i},\quad i=1, \cdots, n %x_{2}&=&\displaystyle\sum_{j=1}^{p}\lambda_{j}\alpha_{2j}+a_{2}\\ %&\vdots&\\ %x_{n} &=&\displaystyle\sum_{j=1}^{p}\lambda_{j}\alpha_{nj}+a_{n} \end{array}%\right. \end{gather*}$}$$
សមីការទម្រង់ដេកាតរបស់លំហអាហ្វីនរង
យក $\vect{\E}$ ជាលំហវ៉ិចទ័កំណត់លើកាយ $\mathbb{K}$ មានវិមាត្រស្មើ $n$ និងកំណត់ $\vect\F$ គឺជាលំហវ៉ិចទ័ររងរបស់ $\vect{\E}$ មានវិមាត្រស្មើ $p$។ ដូច្នេះ មាន $n-p$ ទម្រង់លីនេអ៊ែរ មិនអាស្រ័យលីនេអ៊ែរគ្នា តាងដោយ $\big\{\varphi_{i}\big\}_{i=1}^{n-p}$ ដែលផ្ទៀងផ្ទាត់៖ $$ \forall\ x\in \vect\E,\ x\in \vect\F\quad \Longleftrightarrow \quad \forall\ i,\ \varphi_{i}(x) = 0 $$
Recent Posts
- A Note on the Variation of Parameters Method | 11/01/17
- Group Theory, Part 3: Direct and Semidirect Products | 10/26/17
- Galois Theory, Part 1: The Fundamental Theorem of Galois Theory | 10/19/17
- Field Theory, Part 2: Splitting Fields; Algebraic Closure | 10/19/17
- Field Theory, Part 1: Basic Theory and Algebraic Extensions | 10/18/17