ជំពូក១ : អនុគមន៍
October 2nd, 2020
From Wikipedia:
The volume of this parallelepiped is the absolute value of the determinant of the matrix formed by the columns constructed from the vectors: $\vec r_1, \vec r_2$, and $\vec r_3$.
ក្នុងគណិតវិទ្យា determinant is a scalar value that is a function of the entries of a square matrix. It allows characterizing some properties of the matrix and the linear map represented by the matrix. In particular, the determinant is nonzero if and only if the matrix is invertible and the linear map represented by the matrix is an isomorphism. The determinant of a product of matrices is the product of their determinants (the preceding property is a corollary of this one)
The determinant of $A$ is denoted by $\det(A)$, or it can be denoted directly in terms of the matrix entries by writing enclosing bars instead of brackets: \[ |A| = \begin{vmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{n1}&a_{n2}&\cdots &a_{nn}\end{vmatrix} \] There are various equivalent ways to define the determinant of a square matrix A, i.e. one with the same number of rows and columns: the determinant can be defined via the Leibniz formula, an explicit formula involving sums of products of certain entries of the matrix. The determinant can also be characterized as the unique function depending on the entries of the matrix satisfying certain properties. This approach can also be used to compute determinants by simplifying the matrices in question.
- Use functional notation to evaluate a function.
- Determine the domain and range of a function.
- Verify the following: Draw the graph of a function.
- Find the zeros of a function.
- Recognize a function from a table of values.
- Make new functions from two or more given functions.
- Describe the symmetry properties of a function.
Review of Functions
Functions
Given two sets \(A\) and \(B\) a set with elements that are ordered pairs \((x,y)\) where \(x\) is an element of \(A\) and \(y\) is an element of \(B,\) is a relation from \(A\) to \(B\). A relation from \(A\) to \(B\) defines a relationship between those two sets. A function is a special type of relation in which each element of the first set is related to exactly one element of the second set. The element of the first set is called the input; the element of the second set is called the output. Functions are used all the time in mathematics to describe relationships between two sets. For any function, when we know the input, the output is determined, so we say that the output is a function of the input. For example, the area of a square is determined by its side length, so we say that the area (the output) is a function of its side length (the input). The velocity of a ball thrown in the air can be described as a function of the amount of time the ball is in the air. The cost of mailing a package is a function of the weight of the package. Since functions have so many uses, it is important to have precise definitions and terminology to study them.

Figure \(\PageIndex{1}\): A function can be visualized as an input/output device
A function \(f\) consists of a set of inputs, a set of outputs, and a rule for assigning each input to exactly one output. The set of inputs is called the domain of the function. The set of outputs is called the range of the function.
Figure \(\PageIndex{2}\): A function maps every element in the domain to exactly one element in the range. Although each input can be sent to only one output, two different inputs can be sent to the same output.
For example, consider the function \(f: \mathbb R\to \mathbb R\), where $f(x)=x^2$. Then, the input \(x=3\) is assigned to the output \(3^2=9\).
Since every nonnegative real number has a real-value square root, every nonnegative number is an element of the range of this function. Since there is no real number with a square that is negative, the negative real numbers are not elements of the range. We conclude that the range is the set of nonnegative real numbers.
For a general function \(f\) with domain \(D\), we often use \(x\) to denote the input and \(y\) to denote the output associated with \(x\). When doing so, we refer to \(x\) as the independent variable and \(y\) as the dependent variable, because it depends on \(x\). Using function notation, we write \(y=f(x)\), and we read this equation as “\(y\) equals \(f\) of \(x.”\) For the squaring function described earlier, we write \(f(x)=x^2\).
The concept of a function can be visualized using Figures \(\PageIndex{1}\) - \(\PageIndex{3}\).
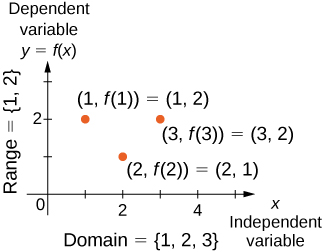
Figure: \(\PageIndex{3}\): In this case, a graph of a function \(f\) has a domain of \(\{1,2,3\}\) and a range of \(\{1,2\}\). The independent variable is \(x\) and the dependent variable is \(y\).
We can also visualize a function by plotting points \((x,y)\) in the coordinate plane where \(y=f(x)\). The graph of a function is the set of all these points. For example, consider the function \(f\), where the domain is the set \(D=\{1,2,3\}\) and the rule is \(f(x)=3−x\). In Figure \(\PageIndex{4}\), we plot a graph of this function.
Figure: \(\PageIndex{4}\): Here we see a graph of the function \(f\) with domain \(\{1,2,3\}\) and rule \(f(x)=3−x\). The graph consists of the points \((x,f(x))\) for all \(x\) in the domain.
Every function has a domain. However, sometimes a function is described by an equation, as in \(f(x)=x^2\), with no specific domain given. In this case, the domain is taken to be the set of all real numbers \(x\) for which \(f(x)\) is a real number. For example, since any real number can be squared, if no other domain is specified, we consider the domain of \(f(x)=x^2\) to be the set of all real numbers. On the other hand, the square root function \(f(x)=\sqrt{x}\) only gives a real output if \(x\) is nonnegative. Therefore, the domain of the function \(f(x)=\sqrt{x}\) is the set of nonnegative real numbers, sometimes called the natural domain.
For the functions \(f(x)=x^2\) and \(f(x)=\sqrt{x}\), the domains are sets with an infinite number of elements. Clearly we cannot list all these elements. When describing a set with an infinite number of elements, it is often helpful to use set-builder or interval notation. When using set-builder notation to describe a subset of all real numbers, denoted \(R\), we write \[\{x\,|\,\; x \text{ has some property}\}\] We read this as the set of real numbers \(x\) such that \(x\) has some property. For example, if we were interested in the set of real numbers that are greater than one but less than five, we could denote this set using set-builder notation by writing \[\{x\,|\,\; 1\lt x \lt 5\} \] A set such as this, which contains all numbers greater than \(a\) and less than \(b\) can also be denoted using the interval notation \((a,b)\). Therefore, \[(1,5)=\{x\,|\,1 \lt x \lt 5\}\] The numbers \(1\) and \(5\) are called the endpoints of this set. If we want to consider the set that includes the endpoints, we would denote this set by writing \[[1,5]=\{x\,|\,1 \le x \le 5\}\] We can use similar notation if we want to include one of the endpoints, but not the other. To denote the set of nonnegative real numbers, we would use the set-builder notation \[\{x\,|\,\; x\ge 0\}\] The smallest number in this set is zero, but this set does not have a largest number. Using interval notation, we would use the symbol \(\infty\) which refers to positive infinity, and we would write the set as \[[0,\infty)=\{x\,|\,\; x\ge 0\}\] It is important to note that \(\infty\) is not a real number. It is used symbolically here to indicate that this set includes all real numbers greater than or equal to zero. Similarly, if we wanted to describe the set of all nonpositive numbers, we could write \[(-\infty,0\,]=\{x\,|\,\; x \leq 0\}\] Here, the notation \(-\infty\) refers to negative infinity, and it indicates that we are including all numbers less than or equal to zero, no matter how small. The set \[(-\infty, \infty)=\{x \,|\,\; x \text{ is any real number}\} \] refers to the set of all real numbers. Some functions are defined using different equations for different parts of their domain. These types of functions are known as piecewise-defined functions. For example, suppose we want to define a function \(f\) with a domain that is the set of all real numbers such that \(f(x)=3x+1\) for \(x \geq 2\) and \(f(x)=x^2\) for \( x\lt 2\). We denote this function by writing \[f(x)=\begin{cases} 3x+1, & \text{if } x\geq 2 \\ x^2, & \text{\; if\; } x\lt 2 \end{cases}\] When evaluating this function for an input \(x\), the equation to use depends on whether \(x\geq 2\) or \(x\lt 2\). For example, since \(5\gt 2\), we use the fact that \(f(x)=3x+1\) for \(x\geq 2\) and see that \(f(5)=3(5)+1=16\). On the other hand, for \(x=-1\), we use the fact that \(f(x)=x^2\) for \(x \lt 2\) and see that \(f(-1)=1\).
For the function \(f(x)=3x^2+2x−1\), evaluate:
- \(f(−2)\)
- \(f(\sqrt{2})\)
- \(f(a+h)\)
Substitute the given value for \(x\) in the formula for \(f(x)\).
- \(f(−2)=3(−2)^2+2(−2)−1=12−4−1=7\)
- \(f(\sqrt{2})=3(\sqrt{2})^2+2\sqrt{2}−1=6+2\sqrt{2}−1=5+2\sqrt{2}\)
- \(f(a+h)=3(a+h)^2+2(a+h)−1=3(a^2+2ah+h^2)+2a+2h−1=3a^2+6ah+3h^2+2a+2h−1\)
For each of the following functions, determine the (i). domain and (ii). range.
- \(f(x)=(x−4)^2+5\)
- \(f(x)=\sqrt{3x+2}−1\)
- \(f(x)=\dfrac{3}{x−2}\)
-
Consider \(f(x)=(x−4)^2+5.\)
- Since \(f(x)=(x−4)^2+5\) is a real number for any real number \(x\), the domain of \(f\) is the interval \((-\infty ,\infty )\).
- Since \((x−4)^2≥0\), we know \(f(x)=(x−4)^2+5≥5\). Therefore, the range must be a subset of \(\{y\,|\,y≥5\}.\) To show that every element in this set is in the range, we need to show that for a given \(y\) in that set, there is a real number \(x\) such that \(f(x)=(x−4)^2+5=y\). Solving this equation for \(x,\) we see that we need \(x\) such that \[(x−4)^2=y−5\] This equation is satisfied as long as there exists a real number \(x\) such that \[x−4=±\sqrt{y−5}\] Since \(y\geq 5\), the square root is well-defined. We conclude that for \(x=4±\sqrt{y−5},\) \(f(x)=y,\) and therefore the range is \(\{y\,|\,y \geq 5 \}\)
-
Consider \(f(x)=\sqrt{3x+2}−1\)
- To find the domain of \(f\), we need the expression \(3x+2≥0\). Solving this inequality, we conclude that the domain is \(\{x\,|\,x≥−2/3\}.\)
- To find the range of \(f\), we note that since \(\sqrt{3x+2}≥0,\) \(f(x)=\sqrt{3x+2}−1≥−1\). Therefore, the range of \(f\) must be a subset of the set \(\{y\,|\,y≥−1\}\). To show that every element in this set is in the range of \(f\), we need to show that for all \(y\) in this set, there exists a real number \(x\) in the domain such that \(f(x)=y.\) Let \(y≥−1.\) Then, \(f(x)=y\) if and only if \[ \sqrt{3x+2}−1=y \] Solving this equation for \(x,\) we see that \(x\) must solve the equation \[\sqrt{3x+2}=y+1\] Since \(y≥−1\), such an \(x\) could exist. Squaring both sides of this equation, we have \(3x+2=(y+1)^2.\) Therefore, we need \[3x=(y+1)^2−2\] which implies \[x=\frac{1}{3}(y+1)^2−\frac{2}{3}\] We just need to verify that \(x\) is in the domain of \(f\). Since the domain of \(f\) consists of all real numbers greater than or equal to \(\frac{−2}{3}\), and \[\frac{1}{3}(y+1)^2-\frac{2}{3}≥−\frac{2}{3}\] there does exist an \(x\) in the domain of \(f\). We conclude that the range of \(f\) is \(\{y\,|\,y≥−1\}\)
- Consider \(f(x)=\dfrac{3}{x−2}.\)
- Since \(3/(x−2)\) is defined when the denominator is nonzero, the domain is \(\{x\,|\,x≠2\}.\)
- To find the range of \(f,\) we need to find the values of \(y\) such that there exists a real number \(x\) in the domain with the property that \[\dfrac{3}{x−2}=y\] Solving this equation for \(x,\) we find that \[x=\dfrac{3}{y}+2\] Therefore, as long as \(y≠0\), there exists a real number \(x\) in the domain such that \(f(x)=y\). Thus, the range is \(\{y\,|\,y≠0\}.\)
Representing Functions
Typically, a function is represented using one or more of the following tools:
- A table
- A graph
- A formula
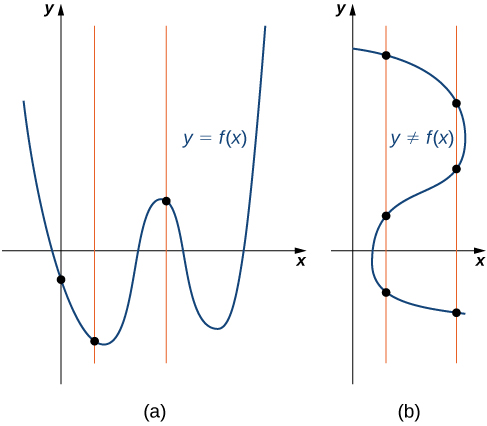
Given a function $f$ , every vertical line that may be drawn intersects the graph of $f$ no more than once. If any vertical line intersects a set of points more than once, the set of points does not represent a function.
We can use this test to determine whether a set of plotted points represents the graph of a function.
Let $f: \mathbb R \longrightarrow \mathbb R$ and $I=[a, b]\subset \mathbb R$. We have following properties:
- We say that a function \(f\) is increasing on the interval \(I\) if for all \(x_{1},\, x_{2}\in I,\) \[f(x_{1})\leq f(x_{2}) \text{ when } x_{1}\lt x_{2}\]
-
We say \(f\) is strictly increasing on the interval \(I\) if for all \(x_{1},x_{2}\in I,\)
\[f(x_{1})\lt f(x_{2}) \text{ when } x_{1}\lt x_{2}\]
- We say that a function \(f\) is decreasing on the interval \(I\) if for all \(x_{1},x_{2}\in I,\) \[ f(x_{1})\geq f(x_{2}) \text{ if } x_{1} \lt x_{2}\]
-
We say that a function \(f\) is strictly decreasing on the interval \(I\) if for all \(x_{1},x_{2}\in I\),
\[f(x_{1})\gt f(x_{2}) \text{ if } x_{1} \lt x_{2}\]
For example, the function \(f(x)=3x\) is increasing on the interval \((-\infty,\infty)\) because \(3x_{1}\lt 3x_{2}\) whenever \(x_{1}\lt x_{2}\). On the other hand, the function \(f(x)=−x^3\) is decreasing on the interval \((−\infty,\infty)\) because \(−x^3_{1}\gt −x^3_{2}\) whenever \(x_{1}\lt x_{2}\) (Figure. 1).
Combining Functions
Now that we have reviewed the basic characteristics of functions, we can see what happens to these properties when we combine functions in different ways, using basic mathematical operations to create new functions. For example, if the cost for a company to manufacture \(x\) items is described by the function \(C(x)\) and the revenue created by the sale of \(x\) items is described by the function \(R(x)\), then the profit on the manufacture and sale of \(x\) items is defined as \(P(x)=R(x)−C(x)\). Using the difference between two functions, we created a new function.
To combine functions using mathematical operators, we simply write the functions with the operator and simplify. Given two functions \(f\) and \(g\), we can define four new functions:
- Sum: \((f+g)(x)=f(x)+g(x)\)
- Difference: \((f−g)(x)=f(x)−g(x)\)
- Product: \((f\cdot g)(x)=f(x) g(x)\)
- Quotient: \(\left(\frac{f}{g}\right)(x)=\frac{f(x)}{g(x)}\) for \(g(x)\neq 0\)
Given the functions \[f(x)=2x−3 \text{ and } g(x)=x^2−1\] find each of the following functions and state its domain. (a) \((f+g)(x)\); (b) \((f−g)(x)\); (c) \((f·g)(x)\); (d) \(\left(\dfrac{f}{g}\right)(x)\)
Recent Posts
- A Note on the Variation of Parameters Method | 11/01/17
- Group Theory, Part 3: Direct and Semidirect Products | 10/26/17
- Galois Theory, Part 1: The Fundamental Theorem of Galois Theory | 10/19/17
- Field Theory, Part 2: Splitting Fields; Algebraic Closure | 10/19/17
- Field Theory, Part 1: Basic Theory and Algebraic Extensions | 10/18/17



