ជំពូក៥ : លំហកុំប៉ាក់

October 2nd, 2020

From Wikipedia:

Per the compactness criteria for Euclidean space as stated in the Heine–Borel theorem, the interval $A = (-\infty, -2]$ is not compact because it is not bounded. The interval $C = (2, 4)$ is not compact because it is not closed. The interval $B = [0, 1]$ is compact because it is both closed and bounded.

In mathematics, specifically general topology, compactness is a property that seeks to generalize the notion of a closed and bounded subset of Euclidean space[1] by making precise the idea of a space having no "holes" or "missing endpoints", i.e. that the space not exclude any "limiting values" of points. For example, the "unclosed" interval $(0,1)$ would not be compact because it excludes the "limiting values" of $0$ and $1$, whereas the closed interval $[0,1]$ would be compact.

Similarly, the space of rational numbers $\mathbb {Q}$ is not compact because it has infinitely many "holes" corresponding to the irrational numbers, and the space of real numbers $\mathbb {R}$ is not compact either because it excludes the limiting values $\infty$ and $-\infty$ . However, the extended real number line would be compact, since it contains both infinities. There are many ways to make this heuristic notion precise. These ways usually agree in Euclidean space, but may be inequivalent in other topological spaces.

Outcomes

Covers of Sets in a Topological Space

The term “cover” is used here to denote an “open cover” when the context is clear and no ambiguity can arise.

(Covers of Sets)

Let $X$ be a topological space and let $A \subseteq X$. Then a Cover/Covering of $A$ is a collection of subsets $\mathcal{F}=\{U_i: i\in I\}$ of $X$ such that $$A \subseteq \bigcup_{i\in I} U_i$$

If $\mathcal{F}$ is a collection of open sets that satisfies the above inclusion then $\mathcal{F}$ is called an Open Cover/Covering of $A$.
Similarly, if $\mathcal{F}$ is a collection of closed sets that satisfies the above inclusion then $\mathcal{F}$ is called a Closed Cover/Covering of $A$.
If $\mathcal{F}^{*} \subseteq \mathcal{F}$ also covers $A$ then we said that $\mathcal{F}^{*} = \{U_{\lambda} : \lambda \in J\subset I\}$ is a Subcover of $A$ from $\mathcal{F}$.

(Cover in the topological space $\mathbb{R}$)

Consider the topological space $\mathbb{R}$ with the usual topology. Let the set $A=\mathbb{N} \subset \mathbb{R}$. Every singleton set in $\mathbb{R}$ is closed and so the collection $\mathcal F = \{\{n\}: n \in \mathbb{N}\}$ is a closed covering of $\mathbb{N}$ since (WHY?):
Let see the collection $\mathcal F=\left\{\left(n-\frac{1}{2}, n+\frac{1}{2}\right): n \in \mathbb{N}\right\}$ is an open covering of $\mathbb{N}$. (WHY?)
For another example, consider the set $A=[0,1) \subset \mathbb{R}$. Then the collection $\mathcal{F}=\left\{\left(-1, \frac{2}{3}\right),\left(\frac{1}{2}, 2\right)\right\}$ is an open cover of $[0,1)$. In general, many open covers for subsets of a topological space may exist.

Show solution

RECALL: (Topological Subspaces). Given the Topological Subspaces $(X, \tau)$ and $A \subseteq X$ then the subspace topology on $A$ is defined to be: $$ \tau_{A}=\{A \cap U: U \in \tau\} $$ We verified that $\tau_{A}$ is indeed a topology for any subset $A$ of $X$. (Can you proof this?)

(topological subspace)

Consider the topological space $(\mathbb{R}, \tau)$ where $\tau$ is the usual topology of open intervals in $\mathbb{R}$. Verify that the subspace topology on $\mathbb{Z} \subseteq \mathbb{R}$ is the discrete topology on $\mathbb{Z}$. (WHY?)

Show solution

(Compactness of Sets)

Let $X$ be a topological space and let $A \subseteq X$. Then $A$ is said to be Compact in $X$ if every open covering of $A$ (from $X$ ) has a finite open subcover.

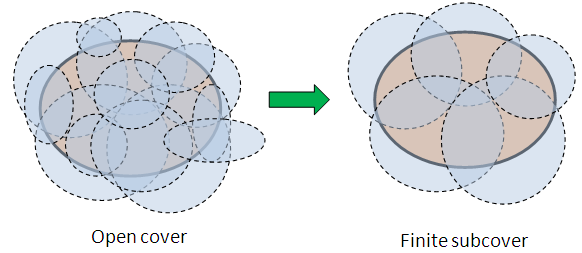
Compactness

READ!.. Please always remember that every closed and bounded interval $[a, b] \subset \mathbb{R}$ (where $\mathbb{R}$ has the usual topology) is compact. In fact, a set $A \subset \mathbb{R}$ is compact if and only if $A$ is both closed and bounded.

More generally, if $\mathbb{R}^{n}$ has the usual topology then $A \subseteq \mathbb{R}^{n}$ is compact if and only if $A$ is both closed and bounded.

In general, it's rather difficult to show that a set is compact and it is usually easier to show that a set is not compact.

(To prove a set is not compact)

consider the set of natural numbers $\mathbb{N} \subset \mathbb{R}$. We claim that $\mathbb{N}$ is not compact in $\mathbb{R}$. To show this, consider the following open cover of $\mathbb{N}$ : $$ \mathcal{F}=\left\{\left(n-\frac{1}{2}, n+\frac{1}{2}\right): n \in \mathbb{N}\right\} $$ (PLEASE EXPLAIN IT!)

Show solution

Theorem 1. : (Compactness of Finite Sets)

Let $X$ be any topological space. If $A \subseteq X$ is a finite set then $A$ is compact in $X$.

Show solution

Lemma : (Compactness of Finite Subsets)

If $X$ is a finite topological space then every subset $A \subseteq X$ is compact in $X$.

Proof: Every subset $A$ of a finite set $X$ is finite. So by Theorem (1) $A$ is compact in $X$.

(Finite Intersection Property)

Let $\mathcal{F}$ be a collection of sets. Then $\mathcal{F}$ is said to have the Finite Intersection Property (FIP) if for every finite collection of sets from $\mathcal{F}$, which is $\left\{F_{1}, F_{2}, \ldots, F_{n}\right\} \subseteq \mathcal{F}$, we have that $$\bigcap_{i=1}^{n} F_{i} \neq \varnothing$$

Theorem 2. : (FIP Criterion for Compactness)

Let $X$ be a topological space. Then $X$ is compact if and only if for every collection of closed sets $\mathcal{F}$ from $X$, we have that \[ \text{ If \;} \mathcal{F} \text{\; has the finite intersection property, then \;\;} \bigcap_{F \in \mathcal{F}} F \neq \varnothing\]

Show proof

$\Rightarrow$ Suppose that $X$ is compact. Let $\mathcal{F}$ be a collection of closed sets from $X$. Suppose that $\mathcal{F}$ has the finite intersection property. Then for every finite subcollection $\left\{F_{1}, F_{2}, \ldots, F_{n}\right\} \subseteq \mathcal{F}$ we have that: $$ \bigcap_{i=1}^{n} F_{i} \neq \emptyset $$ - We want to show that $\bigcap_{F \in \mathcal{F}} F \neq \emptyset$. Suppose not, i.e., suppose that: $$ \bigcap_{F \in \mathcal{F}} F=\emptyset $$ - Then taking the complement of both sides above and using De Morgan's laws and we see that: $$ \begin{gathered} \left(\bigcap_{F \in \mathcal{F}} F\right)^{c}=\emptyset^{c} \\ \bigcup_{F \in \mathcal{F}} F^{c}=X \end{gathered} $$ - Since $F$ is closed for all $F \in \mathcal{F}$ we have that $F^{c}$ is open for all $F \in \mathcal{F}$. So $\left\{F^{c}: F \in \mathcal{F}\right\}$ is an open cover of $X$. Since $X$ is compact, there exists a finite subcover, say $\left\{F_{1}^{c}, F_{2}^{c}, \ldots, F_{n}^{c}\right\} \subseteq\left\{F^{c}: F \in \mathcal{F}\right\}$ such that: $$ \bigcup_{i=1}^{n} F_{i}^{c}=X $$ - Taking the complement of both sides again and using De Morgan's laws and we have that: $$ \begin{array}{r} \left(\bigcup_{i=1}^{n} F_{i}^{c}\right)^{c}=X^{c} \\ \bigcap_{i=1}^{n} F_{i}=\emptyset \end{array} $$ - But then $\left\{F_{1}, F_{2}, \ldots, F_{n}\right\}$ is a finite collection of sets from $\mathcal{F}$ that does not have the finite intersection property which is a contradiction. Hence the assumption that $\bigcap_{F \in \mathcal{F}} F=\emptyset$ was false. So $\bigcap_{F \in \mathcal{F}} F \neq \emptyset$.

$\Leftarrow$ Suppose that if for every collection $\mathcal{F}$ of closed sets from $X$ we have that if $\mathcal{F}$ has the finite intersection property then $\bigcap_{F \in \mathcal{F}} F \neq \emptyset .$ - Let $\left\{A_{i}: i \in I\right\}$ be an open cover of $X$. Then: $$ \bigcup_{i \in I} A_{i}=X $$ - Suppose $X$ is not compact. Then for all finite subsets $J \subseteq I$ we have that: $$ \bigcup_{i \in J} A_{i} \neq X $$ - Taking the complement of both sides of the equation above and using De Morgan's laws shows us that: $$ \begin{array}{r} \left(\bigcup_{i \in J} A_{i}\right)^{c} \neq X^{c} \\ \bigcap_{i \in J} A_{i}^{c} \neq \emptyset \end{array} $$ - So $\left\{A_{i}^{c}: i \in I\right\}$ has the finite intersection property. Therefore: $$ \bigcap_{i \in I} A_{i}^{c} \neq \emptyset $$ - Taking the complement of both sides of the equation above and using De Morgan's laws gives: $$ \begin{array}{r} \left(\bigcap_{i \in I} A_{i}^{c}\right)^{c} \neq \emptyset^{c} \\ \bigcup_{i \in I} A_{i} \neq X \end{array} $$ - But this contradicts $\left\{A_{i}: i \in I\right\}$ being an open cover of $X$. Hence the assumption that $X$ is not compact was false. Therefore $X$ is compact.

Preservation of Compactness under Continuous Maps

We will see in the following theorem, compactness is preserved under continuous maps, i.e., if $X$ and $Y$ are topological spaces, and $A \subseteq X$ is compact in $X$, and $f: A \rightarrow Y$ is a continuous map, then the image $f(A)$ will also be compact in $Y$.

Theorem 3. : (Preservation of Compactness)

Let $X$ and $Y$ be topological spaces, $A \subseteq X$, and $f: A \rightarrow Y$ be a continuous map. If $A$ is compact in $X$ then $f(A)$ is compact in $Y$.

Theorem 1. : (Compactness of Finite Sets)

()

Show proof

ជំពូក៥ : លំហកុំប៉ាក់

Outcomes

Covers of Sets in a Topological Space

Preservation of Compactness under Continuous Maps

Recent Posts